Пусть в равнобедренном треугольнике АВС с основанием AB: АС=СВ=a, AB=b. <A=<B, SinA=SinB=1/4. Тогда CosB=√(1-1/16)=√15/4. По теореме косинусов из треугольника АВС имеем: a²=a²+b²-2abCosB или 0=b²-2*16√15*b*√15/4 или b²-120b=0. b1=0 - не удовлетворяет условию. b=120. Площадь треугольника АВС равна: (1/2)*a*b*sinA или Sabc=(1/2)*16√15*120*0,25=240√15. С другой стороны Sabc=(1/2)*a*h, где а - сторона ВС, h - высота АН, проведенная к этой стороне. Тогда АН=2Sabc/a или АН=480√15/(16√15)=30. ответ: АН=30.
P.S. Заметим, что треугольник АВС - тупоугольный, так как синус угла при основании равен 0,25 => угол ≈14,5°.
1. Правильный четырехугольник - квадрат.
Диаметр вписанной в квадрат окружности равен стороне квадрата. ⇒ r=d:2=4:2=2 см.
Для описанного вокруг данной окружности треугольника АВС она - вписанная.
Радиус вписанной в правильный треугольник окружности равен 1/3 его высоты. Следовательно, высота ∆ АВС =2•3=6 см.
Тогда АВ=ВН:sin60°=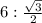
=4√3 см.
* * *
2. Для нахождения площади сектора существует формула.
S=Lr:2, где L – длина дуги сектора. ⇒
S=6•4:2=12 см²
Если формула забыта, решить задачу можно без нее.
Длина окружности C=2πr
C=2•p•4=8π см
Площадь окружности S=πr²=16 π см²
Вычислим площадь, которая приходится на сектор с дугой в 1 см.
S:C=16π:8π=2
Тогда площадь сектора
S=2•6=12 см²
АС=СВ=a, AB=b. <A=<B, SinA=SinB=1/4.
Тогда CosB=√(1-1/16)=√15/4.
По теореме косинусов из треугольника АВС имеем:
a²=a²+b²-2abCosB или 0=b²-2*16√15*b*√15/4 или
b²-120b=0. b1=0 - не удовлетворяет условию.
b=120.
Площадь треугольника АВС равна: (1/2)*a*b*sinA или
Sabc=(1/2)*16√15*120*0,25=240√15. С другой стороны
Sabc=(1/2)*a*h, где а - сторона ВС, h - высота АН, проведенная к этой стороне. Тогда
АН=2Sabc/a или АН=480√15/(16√15)=30.
ответ: АН=30.
P.S. Заметим, что треугольник АВС - тупоугольный, так как синус угла при основании равен 0,25 => угол ≈14,5°.