Задача №1 Даны три последовательные вершины параллелограмма А(1;2), В(-1;3), С(-4;2). Не находя координаты вершины D, найти:

- уравнение стороны AD;

- уравнение высоты ВК, опущенной из вершины В на сторону AD;

- длину высоты ВК;

- уравнение диагонали BD;

- тангенс угла между диагоналями параллелограмма;

- косинус угла В параллелограмма.

Записать общие уравнения найденных прямых.

Объяснение:

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.

1) прямая DC1 и плоскость A1B1C1

DD1 ⊥ (A1B1C1) ⇒ DD1 ⊥ D1C1 ⇒ D1C1  - проекция прямой DC1 на плоскость A1B1C1, а ∠DС1D1 - искомый угол.

Рассмотрим ΔDС1D1 (∠D1=90°):  

D1C=A1B1=AB=5

DD1=AA1=12

tg ∠DС1D1 = D1D1/C1D1 = 12/5

∠DС1D1 = arctg (12/5)

2) прямая B1D и плоскость ABC

BB1 ⊥ (ABC) ⇒ BB1 ⊥ BD ⇒ BD  - проекция прямой B1D на плоскость ABC, а ∠B1DB- искомый угол.

Рассмотрим ΔB1DB (∠B=90°):

BB1=AA1=12

BD найдём из прямоугольного ΔABD(∠A=90°) по т.Пифагора:

BD² =AB²+AD²=25+49=74

tg ∠B1DB=BB1/BD=   = =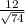

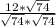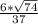
∠B1DB= arctg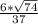

Из ∆АВС: ∠В=30, ∠А=60°

Из ∆АВД: ∠АВД=15°, ∠АДВ=105°

Из ∆СВД: ∠СВД=15°, ∠ВДС=75°

Объяснение:

Сумма смежных углов составляет 180°, а ∠ВАЕ смежный с ∠ВАС, значит

∠ВАС=180–∠ВАЕ=180–120=60°

Рассмотрим ∆АВС, он прямоугольный, с прямым ∠С=90°. Сумма острых углов прямоугольного треугольника равна 90°, тогда

∠АВС=90–∠ВАС=90–60=30°

Из условия известно что ВД - биссектриса и делит ∠В пополам, поэтому

∠АВД=∠СВД=30÷2=15°

Рассмотрим ∆АВД, в нём ∠ВАД=60°, ∠АВД=15°. Сумма углов треугольника составляет 180°, значит

∠АДВ=180–∠ВАД–∠АВД=180–60–15=105°

∠ВДС смежный с ∠АДВ, тогда

∠ВДС=180–105=75°