Задача 1
В прямоугольнике КМNP проведена биссектриса угла МКP,
которая пересекает сторону МN в точке Е.
Найдите сторону КP, если МЕ = 14 см, а периметр прямоугольника
КМNP
равен 62 см.
Задача 2
Одна из сторон параллелограмма в 3 раза меньше другой, а
периметр параллелограмма равен 36 см. Вычислите, чему равны
стороны параллелограмма.
Задача 3
В трапеции АВСД основание АД образует с боковыми сторонами
АВ и СД углы, равные 700 и 450 . Определите остальные углы
трапеции.
Задача 4
В прямоугольнике АВСД сторона АВ равна 22 см, а угол АВД равен
600 Найдите диагональ АС.
Задача 5
В параллелограмме АВСД периметр равен 60см. ∠С=30°, а
перпендикуляр к прямой АД равен 12см. Найти углы и стороны
параллелограмма.
Задача 6
Найдите меньшее основание равнобедренной трапеции, если ее
большее основание равно 25 см, боковая сторона – 11 см, а один из
углов равен 60°.
92,8 см
Объяснение:
Так как MNKL - прямоугольник, то его противоположные стороны попарно равны: MN = KL, NK = ML.
Диагонали прямоугольника равны: МК=NL.
Q, R, S и T - середины сторон прямоугольника ⇒
MQ=QN=KS=SL, NR=RK=MT=TL.
Средняя линия треугольника — отрезок, который соединяет середины двух сторонQR - средняя линия ΔMNK, RS - средняя линия ΔNKL, TS-средняя линия ΔMKL, QT- средняя линия ΔNML.
Средняя линия параллельна третьей стороне, а ее длина равна половине длины этой стороныQR =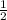
* МК = 
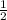* 46,4 = 23,2 см
TS =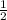
* МК = 
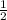* 46,4 = 23,2 см
RS =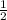
* NL = 
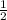* 46,4 = 23,2 см
QT =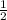
* NL = 
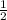* 46,4 = 23,2 см
Периметр четырёхугольника QRST:
Р=QR+TS+RS+QT=4*23,2=92,8 см
20,5
Объяснение:
Точки K и L — середины сторон AB и BC соответственно.
KL - это средняя линия.
Средняя линия параллельна противолежащей стороне и равна ее половине.KL || AC
∠AKD=∠LKD - по условию∠KLD=∠DLC - по условию∠LKD=∠KDA - как накрест лежащие углы при KL || AC и секущей KD
∠KLD=∠LDC - как накрест лежащие углы при KL || AC и секущей LD
Значит, ∠AKD=∠LKD=∠KDA и ∠KLD=∠DLC=∠LDC
⇒ ΔAKD и ΔCDL - равнобедренные ⇒ KA=AD, LC=CD
Значит, KA=AD=BK, LC=CD=BL
AC=AD+CD=(1/2)·AB + (1/2)·BC=(1/2)·(AB+BC)=(1/2)·41=20,5