задача:Известно, что DE||AC. Найдите длинну BE, если BC=42cm,DE=12cm,AB=24cm 2 Задача Известно, что DE||AC. Найдите длинну ED, если BD=9cm,BA=27 cm, AC=24cm
А) По известной теореме через центр симметрии и данную прямую можно провести единственную плоскость.
Пусть О — центр симметрии, а — данная прямая, α — плоскость, проведенная через О и а.
Пусть А ∈ а, построим отрезок ОА.
Продолжим ОА за точку О на расстояние ОА1=АО. Получим точку А1, симметричную А.
Пусть В ∈ а, построим отрезок ОВ. Продолжим ОВ за точку О на расстояние ОВ1=ОВ. Получим точку B1, симметричную точке В.
Через А1 и В1 проведем прямую b. Рассмотрим ΔAОВ и ΔА1ОВ1⋅AО=А1О, ВО=ОВ1, ΔАОВ=ΔА1ОВ1 как вертикальные, следовательно, ΔAОВ=ΔА1ОВ1.
Тогда, ∠1=∠2 и а || b.
б) Пусть А ∈ а. Симметричная ей точка А1 тоже принадлежит прямой а; АО=ОА1.
Точка А произвольна, следовательно, любая точка прямой, а также симметричная точка относительно центра О лежат на прямой а, следовательно, прямая а переходит сама в себя при условии, что проходит через центр симметрии.
Пирамида MABCD - правильная, в основании лежит квадрат ABCD,
AB=BC=CD=AD=6 см, боковые рёбра равны AM = BM = CM = DM, высота опускается в точку пересечения диагоналей квадрата.
Диагональ квадрата равна d = a√2 :
AC = AB · √2 = 6√2 см
Диагонали квадрата точкой пересечения делятся пополам :
OC = AC : 2 = 6√2 : 2 = 3√2 см
ΔMOC - прямоугольный равнобедренный, так как
∠CMO = ∠MCO = 45° ⇒ OM = OC = 3√2 см
MK - апофема боковой грани AMD
ΔMOK - прямоугольный, KO = AB:2 = 6:2 = 3 см
По теореме Пифагора
MK² = OM² + KO² = (3√2)² + 3² = 18 + 9 = 27
MK = √27 = 3√3 см
Sбок =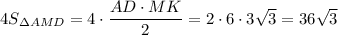 см²
см²
ответ : 36√3 см²
Пусть О — центр симметрии, а — данная прямая, α — плоскость, проведенная через О и а.
Пусть А ∈ а, построим отрезок ОА.
Продолжим ОА за точку О на расстояние ОА1=АО. Получим точку А1, симметричную А.
Пусть В ∈ а, построим отрезок ОВ. Продолжим ОВ за точку О на расстояние ОВ1=ОВ. Получим точку B1, симметричную точке В.
Через А1 и В1 проведем прямую b. Рассмотрим ΔAОВ и ΔА1ОВ1⋅AО=А1О, ВО=ОВ1, ΔАОВ=ΔА1ОВ1 как вертикальные, следовательно, ΔAОВ=ΔА1ОВ1.
Тогда, ∠1=∠2 и а || b.
б) Пусть А ∈ а. Симметричная ей точка А1 тоже принадлежит прямой а; АО=ОА1.
Точка А произвольна, следовательно, любая точка прямой, а также симметричная точка относительно центра О лежат на прямой а, следовательно, прямая а переходит сама в себя при условии, что проходит через центр симметрии.