проекция вершины s на основание , есть точка пересечения диагоналей квадрата abcd .
положим что это точка h .
l,k середины as, cs соответсвенно , также положим что b1k пересекает bc в точке x , можно теореме менелая , тогда
bb1/b1s * sk/kc * cx/bx=1
или (20-5)/5*(1/1)* (cx/(24+cx))=1 , откуда cx=12 , значит bx=36. аналогично если y точка пересечения lb1 с ab , тогда by=36 .
опустим высоту из точки b1 на основание , основание высоты n будет лежат на диагонали . найдём b1n , подобия треугольников shb и b1nb , тогда sh/b1n = 4/3
по теореме пифагора sh=sqrt(bs^2 - bh^2) = sqrt(bs^2-(bd/2)^2) = sqrt(20^2-(12 sqrt()= sqrt(112) , значит b1n = 3*sqrt(7) и bn=sqrt(15^2-9*7)=9*sqrt(2) . xby равнобедренный и прямоугольный треугольник , положим что m точка пересечения bn и xy , тогда bm=36*sqrt(2) , и mn=bm-bn= 36*sqrt(2)-9*sqrt(2) = 27*sqrt(2) .
тогда если "a" это угол между плослкостью основания и данной плосокостью то
tga=b1n/mn = 3*sqrt(7) / 27*sqrt(2) = sqrt(14)/18 , откуда
Четырёхугольник ABCD - равнобедренная трапеция (ВС║AD, AD > ВС, АВ = CD).
Отрезок ВН - высота, опущенная на основание AD (ВН⊥AD, ВН⊥ВС).
Отрезок МК - средняя линия.
AH : HD = 1 : 5.
HD = 35 см.
Найти :МК = ?
Решение :На основание AD из вершины тупого ∠С опустим высоту СН₁ (СН₁⊥AD, СН₁⊥ВС).
По свойству отрезков в равнобедренной трапеции, образованных основанием высоты на большем основании :
АН = DH₁.
Пусть АН = х, тогда, по условию задачи, HD = 5х.
HD = 5х
35 см = 5х
х = 35 см/5
х = 7 см.
АН = DH₁ = х = 7 см
AD = AH + HD = 7 см + 35 см = 42 см.
Рассмотрим четырёхугольник BHH₁C.
Все его углы прямые, значит, этот четырёхугольник - прямоугольник (признак прямоугольника).
AD = AH + HH₁ + DH₁
HH₁ = AD - AH - DH₁ = 42 см - 7 см - 7 см = 28 см.
Тогда ВС = НН₁ = 28 см (так как противоположные стороны прямоугольника равны).
Средняя линия трапеции равна полусумме её оснований.Следовательно :
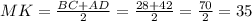 cм.
cм.
ответ :35 см.
відповідь:
пояснення:
проекция вершины s на основание , есть точка пересечения диагоналей квадрата abcd .
положим что это точка h .
l,k середины as, cs соответсвенно , также положим что b1k пересекает bc в точке x , можно теореме менелая , тогда
bb1/b1s * sk/kc * cx/bx=1
или (20-5)/5*(1/1)* (cx/(24+cx))=1 , откуда cx=12 , значит bx=36. аналогично если y точка пересечения lb1 с ab , тогда by=36 .
опустим высоту из точки b1 на основание , основание высоты n будет лежат на диагонали . найдём b1n , подобия треугольников shb и b1nb , тогда sh/b1n = 4/3
по теореме пифагора sh=sqrt(bs^2 - bh^2) = sqrt(bs^2-(bd/2)^2) = sqrt(20^2-(12 sqrt()= sqrt(112) , значит b1n = 3*sqrt(7) и bn=sqrt(15^2-9*7)=9*sqrt(2) . xby равнобедренный и прямоугольный треугольник , положим что m точка пересечения bn и xy , тогда bm=36*sqrt(2) , и mn=bm-bn= 36*sqrt(2)-9*sqrt(2) = 27*sqrt(2) .
тогда если "a" это угол между плослкостью основания и данной плосокостью то
tga=b1n/mn = 3*sqrt(7) / 27*sqrt(2) = sqrt(14)/18 , откуда
a=arctg(sqrt(14)/18) .