Задача по трапеции...

Немного теории:  

Для обозначения геометрических фигур и их проекций, для отображения отношения между геометрическими фигурами, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем используются символьные обозначения.

- Большими латинскими буквами A, B, C, D, ..., L, M, N, ... - обозначают  точки расположенные в пространстве;

- малыми латинскими буквами a, b, c, d, ..., l, m, n, ... - обозначают  линии, расположенные в пространстве;

- малыми греческими буквами α, β, γ, δ, ..., ζ, η, θ - обозначают плоскости;

∈, ⊂ , ⊃ - Такими знаками обозначают принадлежность точек прямой и прямых плоскости

Теперь Задание:

1 точка M принадлежит плоскости альфа но не принадлежит плоскости бета  

α, β, плоскости, М- точка

М∈α, М∉β

2 прямая l и точка N не лежащая на прямой l. принадлежат плоскости бета

N∉l; N∈α; l⊂α

45°

Объяснение:

АВСД-ромб. АС⊥ВД. АС=40см. ВД=30см.

Из вершины В ромба АВСД проведём высоту ВК⊥ДС.

МК - наклонная, ВК - её проекция на плоскость АВСД.

По теореме о трёх перпендикулярах: МК⊥ДС.

∠МКБ - угол между плоскостью ромба и плоскостью CMD - искомый угол.

(Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.)

1) ΔОВС (∠О=90° - как угол между диагоналями ромба).

По т.Пифагора найдём сторону ромба:

ВС² = ВО²+ОС² = 15²+20²=625, ВС= 25 см

Т.е. АВ=ВС=СД=АД=25 см - как диагонали ромба

2) ΔВСД .

СО⊥ВД т.к. диагонали ромба пересекаются под прямым углом.

ВК⊥ДС по построению.

Площадь ΔВСД:  

S =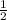 *ВД*ОС

S =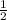 *ДС*ВК

⇒ВД*ОС=ДС*ВК;   30*20=25*ВК; ВК=30*20/25=24 см

3) Рассмотрим ΔМВК.    МВ⊥ВК, МВ=ВК=24 см.

⇒ΔМВК - равносторонний прямоугольный треугольник.

∠КМВ =∠МКВ = 90°/2 = 45°