Очевидно, что одной из сторон треугольника, которая равна 4 см, является сторона, проекция которой равна 3 см.
В противном случае, если бы это была другая сторона, то треугольник прекратился бы в линию, так как длина стороны (4 см) и её проекция (4 см) были бы равны.
1) В прямоугольном треугольнике сторона 4 см является гипотенузой, а её проекция (3 см) является катетом. По теореме Пифагора находим высоту:
h = √(4²-3²)= √(16-9) = √7 см.
2) Соответственно третья сторона х, которую необходимо найти, является гипотенузой в прямоугольном треугольнике с катетом
h =√7см и другим катетом 4 см (проекцией этой стороны на большую сторону треугольника):
√23 см ≈ 4,8 см.
Объяснение:
Очевидно, что одной из сторон треугольника, которая равна 4 см, является сторона, проекция которой равна 3 см.
В противном случае, если бы это была другая сторона, то треугольник прекратился бы в линию, так как длина стороны (4 см) и её проекция (4 см) были бы равны.
1) В прямоугольном треугольнике сторона 4 см является гипотенузой, а её проекция (3 см) является катетом. По теореме Пифагора находим высоту:
h = √(4²-3²)= √(16-9) = √7 см.
2) Соответственно третья сторона х, которую необходимо найти, является гипотенузой в прямоугольном треугольнике с катетом
h =√7см и другим катетом 4 см (проекцией этой стороны на большую сторону треугольника):
х = √((√7)²+4²) = √(7+16) = √23 см ≈ 4,8 см.
ответ: √23 см ≈ 4,8 см.
Площадь прямоугольника находится по формуле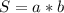
, т.е. просто перемножаем две соседние стороны.
Известно, что стороны
и 
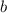соотносятся друг к другу как 3:2. Давайте обозначим стороны за x.
Просто перемножим эти значения, найдём x и потом подставим.
Поскольку длина стороны не может быть отрицательной, то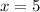
.
Теперь подставим полученное значение x в
и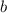 
.
Готово!
ответ: a = 15 см; b = 10 см.
ПроверкаДавайте проверим, правильное ли решение.
Просто воспользуемся формулой, которую я привёл в самом начале.
ответ верный!