задание 243. В треугольнике ABC из вершины А на сторону ВС проведена высота
AD, при этом 2CAD = 46° и 2BAD = 27°. Найти углы треугольника.
| 730, 44°; 63°
задание 244.В треугольнике ABC высота BD делит 2В на ZABD: 2CBID 2:3, а
C = 54°. Найти А и В.
669, 60°
задание 245. В треугольнике ABC высота BD делит ZB на два, один из которых
ZABD меньше 2CBD на 11°. Найти 2В и ДС, если мало времени
1) Треугольники вне восьмиугольника равны по двум сторонам и углу между ними(по свойству правильного многоугольника), значит стороны вписанного многоугольника равны, а т.к. его стороны равны, то это правильный восьмиугольник.
2)В треугольнике АВМ:АД-высота(т.к.угол АДМ=90), также АД является медианой этого треугольника(ВД=МД по условию) из этого следует, что треугольник АВМ-равнобедренный. Тогда АВ=АМ=4. И т.к. АМ=МС, АС=АМ+МС=4+4=8.
3)Треугольники вне восьмиугольника равны по двум сторонам и углу между ними(по свойству правильного многоугольника), значит стороны вписанного четырехугольника равны, и это значит, что это четырехугольник-ромб, т.к. диагонали правильного восьмиугольника равны, то и в ромбе диагонали равны, из чего следует, что это квадрат.
4)Обозначим СД=х.Проведем высоты ВН1 и СН2, угол ДСН2=90-60=30. Тогда ДН2=1/2 СД=х/2. Т.к. АД=2х, то АН1=2х-х-х/2=х/2, из этого следует, что трапеция равнобедренная, а значит СД=2. Тогда АД=2СД=2*2=4. СН2=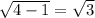
. S=СН2*АД=корень из 3*4=4 корня из 3
Пусть ВМ и АD пересекаются в точке Н.
Медиана ВМ делит АС на два равных отрезка АМ=СМ.
АМ=4:2=2
АН в треугольнике АВМ является высотой - угол АНВ - прямой , т.к. АD перпендикулярна ВМ.
Но она же и медиана, т.к. по условию ВН=НМ, следовательно, треугольник ВАМ - равнобедренный
( в равнобедренном треугольнике медиана, высота и биссектриса, проведенные из вершины угла против основания - совпадают, и, наоборот, если медиана и высота треугольника равны, то этот треугольник - равнобедренный).
АВ=АМ=2
( с нескольких попыток не удалось загрузить рисунок, но он очень простой, несложно выполнитьсамостоятельно)