Задание к чертежам: найти пары равных тре- угольников и доказать их равенство.
Теория к заданиям:
D
2
І признак: если два угла одного
треугольника соответственно раины
двум углам другого, то такие тре-
угольники подобны (рис. 42).
2A - Ay 2В - В.
ДА
BA,
B:
M
Конец документа
R
Р
Х
N N
аны 1-2 из 2​

(-2,2; -0,6)

Объяснение:

Пусть точка P(x₀, y₀) удовлетворяет системе уравнений. Возьмём квадратный корень из левой и правой части каждого уравнения:

Первое уравнение задаёт расстояние от точки P(x₀, y₀) до точки A(-4, -3), равное трём. Второе уравнение задаёт расстояние от точки P(x₀, y₀) до точки B(-1, 1), равное двум.

Заметим, что расстояние между точками A(-4, -3) и B(-1, 1) равно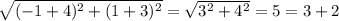 . Расстояние между данными точками равно сумме расстояний между точками P(x₀, y₀) и A(-4, -3) и между точками P(x₀, y₀) и B(-1, 1) (AB (5) = AP (3) + PB (2)). Значит, точка P(x₀, y₀) находится на отрезке между точками A(-4, -3) и B(-1, 1) и делит его в отношении 3 : 2, считая от точки A(-4, -3). Тогда справедливо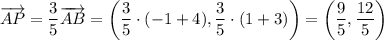

Поскольку точка A находится не в начале координат, выполнив параллельный перенос на вектор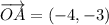 , мы получим координаты точки P(x₀, y₀): .

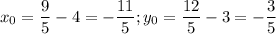Решением системы является точка (-2,2; -0,6).

Відповідь:

Пояснення:

1.12

вопрос 3

квадрат

вопрос 4

Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

вопрос 5

диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам

Вопрос 6

Объём параллелепипеда равен произведению площади основания на высоту. ДА

Куб - это прямоугольный параллелепипед, все рёбра которого равны, то есть все грани которого - равные квадраты. НЕТ

Параллелепипеды бывают наклонные, прямые и прямоугольные. ДА

Если у параллелепипеда боковые грани расположены по отношению к основаниям под углом равным 90о, то он называется наклонным. НЕТ

Вопрос 7

добутку вох граней паралелепіпеда

суме всех площадей

добутку трьох граней

поднести грань к кубу

вопрос 8

(10*10+10*8+8*10)*2 =520