Проведём высоты СН и DН основания пирамиды и боковой грани, соответственно. Двугранный угол при стороне основания, равный 45 градусов, это и есть линейный угол DНС.
Вершина правильной пирамиды проецируется в центр основания, в нашем случае это точка пересечения медиан (и биссектрис и высот в одном лице).
Рассмотрим ΔDОН (на рисунке - жёлтым):
Он прямоугольный, один из острых углов равен 45⁰, значит это равнобедренный треугольник, ОН=ОD=6 см.
Таким образом, высота боковой грани DH равна:
см
Теперь находим сторону основания.
Вспоминаем, что медианы треугольника точкой пересечения делятся на две части в отношении 2:1, считая от вершины.
Значит медиана СН=6*3=18 см
В ΔАНС (на рисунуе - зелёным) угол НСА=30⁰, значит
Обозначив сторону основания за Х, получим уравнение:
Вообще есть одна формула, которая находит сторону куба через его диагональ. Но чтобы понятней было представлю рисунок. Дано: Куб Сторона-х Диагональ=10см Решение: 1,Для начала найдем диагональ основания куба из равнобедренного прямоугольного треугольника. Пусть диагональ основания L . Применим теорему Пифагора x²+x²=L² L²=2x² L=x√2
2.Теперь через еще один прямоугольный треугольник, в котором гипотенуза=d Найдем сторону x²+(x√2) ²=d² 3x²=d² Из этого выходит формула, где сторона выражается через диагональ d=x√3 10=x√3 x=10/√3 3. S полной поверхности куба - это сумма площадей всех его граней, их всего 6 и они одинаковы. S=6x² S=6*100/2=300 4. V=x³ V=1000/3√3=1000√3/3≈333,3√3
Проведём высоты СН и DН основания пирамиды и боковой грани, соответственно. Двугранный угол при стороне основания, равный 45 градусов, это и есть линейный угол DНС.
Вершина правильной пирамиды проецируется в центр основания, в нашем случае это точка пересечения медиан (и биссектрис и высот в одном лице).
Рассмотрим ΔDОН (на рисунке - жёлтым):
Он прямоугольный, один из острых углов равен 45⁰, значит это равнобедренный треугольник, ОН=ОD=6 см.
Таким образом, высота боковой грани DH равна:
Теперь находим сторону основания.
Вспоминаем, что медианы треугольника точкой пересечения делятся на две части в отношении 2:1, считая от вершины.
Значит медиана СН=6*3=18 см
В ΔАНС (на рисунуе - зелёным) угол НСА=30⁰, значит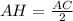
Обозначив сторону основания за Х, получим уравнение:
Находим площадь боковой поверхности:
Дано:
Куб
Сторона-х
Диагональ=10см
Решение:
1,Для начала найдем диагональ основания куба из равнобедренного прямоугольного треугольника. Пусть диагональ основания L .
Применим теорему Пифагора
x²+x²=L²
L²=2x²
L=x√2
2.Теперь через еще один прямоугольный треугольник, в котором гипотенуза=d
Найдем сторону
x²+(x√2) ²=d²
3x²=d²
Из этого выходит формула, где сторона выражается через диагональ
d=x√3
10=x√3
x=10/√3
3. S полной поверхности куба - это сумма площадей всех его граней, их всего 6 и они одинаковы.
S=6x²
S=6*100/2=300
4. V=x³
V=1000/3√3=1000√3/3≈333,3√3