задания
распишите по действия плс

ответ: отвечу пока на 2 первых задачи

Объяснение: ЗАДАНИЕ 1

Чтобы найти полную площадь поверхности цилиндра -это сумма его площадей основ и боковой поверхности:

Sпол=S2-х.осн+ Sбок

Диагональ с основание образуют прямоугольный треугольник, в котором один из острых углов составляет 45°, тогда угол 45° эта диагональ образует и с верхним основание цилиндра, поэтому этот прямоугольный треугольник- равнобедренный, и те стороны, к которым прилегают углы 45°, тоже равны. Поэтому диаметр нижнего основания= высоте цилиндра:(Диаметр=2r=7×2=14см)

Площадь основания=πr²=π×7²=49π(см²)

Так как у нас 2 таких основания, то вместе их сумма составит 2×49π=98π(см²)

Итак: S2-х.осн=98π(см²)

Площадь боковой поверхности вычисляется по формуле: Sбок=2πr×h, где h-высота цилиндра.

Sбок=2π×7×14=14π×14=196π(см²)

Sбок=196π(см²)

Теперь найдём полную площадь поверхности цилиндра, зная площадь боковой поверхности и площадь оснований:

Sпол=Sбок+S2-х.осн=196π+98π=294π(см²)

ОТВЕТ: Sпол=294(см²)

ЗАДАНИЕ 2

Осевым сечением усечённого конуса является трапеция, т.е. нам нужно найти площадь трапеции. Её площадь вычисляется по формуле: (а²+b²)/2×h, где а и b- основания трапеции, а h- её высота.

Рассмотрим обычную трапецию и Обозначим её вершины А В С Д, где ВС и АД - её основания, а АВ и СД- боковые стороны. Трапеции равнобедренная, поэтому АВ=СД=10дм, а радиусы оснований равны половинам её основ: ВС=10×2=20дм;

АД=18×2=36дм.

Проведём из вершины В и С две высоты ВН и СН1, к основанию АД. Они делят АД так что НН1=ВС=20дм. Так как трапеция равнобедренная, то

АН = ДН1=(36-20)/2=16/2=8дм

Рассмотрим полученный ∆АВН. Он прямоугольный, где ВН и АН - катеты, а АВ - гипотенуза. По теореме Пифагора найдём высоту ВН:

ВН²=АВ²-АН²=10²-8²=100-64=36;

ВН=√36=6дм

Теперь найдём площадь трапеции зная высоту и оба основания:

Sтрап=(20+36)/2×6=56/2×6=28×6=168дм²

ОТВЕТ: площадь трапеции или площадь осевого сечения цилиндра: Sсеч=168дм²

1) Объём конуса равен (формула) (1/3)π*R²*h

R - радиус

h - высота

Теорема Пифагора в этом случае: R² + h²=L², выразим R² = (L²- h²) м²

Получилось, что V = (π*( L² - h²)*h)/3 = (π/3)*( L²*h - h³) м³.  

Далее: V'(h) = (π/3)*( L² - 3h²).  (Это производная)

Нужно прировнять производную к нулю, видим: (π/3)*( L² - 3h²) = 0.  

Теперь и второе выражение приравниваем к нулю:

И выражаем: h = √(( L²)/3) = L/√3 = 22,8/√3 примерно равно 4,77493 см.

h у нас положительно число (т.е больше нуля) получается, что: h= (L/√3)! Максимальная!

4,77/√3=(примерно)3.

И нужно подставить значение высоты: h = (L/√3) в уравнение объёма:

V = (π/3)*(L²*(L/√3)-(L/√3)³) = (2π*L3)/(3*√3).

Получаем то, что

V = (2π*22,8*3)/(2/√3) примерно получаем 118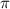 cм³.  

ответ: 118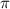

А, если посчитать с числом пи, то получим примерно 371 см²