Закінчіть речення: А) Коло називають вписаним у трикутник, якщо ... Б) Центром кола, вписаного у трикутник, є ... В) Дотик двох кіл називають зовнішнім, якщо ... Г) Дотик двох кіл називають внутрішнім, якщо ...
1. Треугольники АВС и MNK подобны. ∠А = ∠М. ВС = 8, NK = 2. Площадь треугольника MNK равна 12 (ед²). Найдите площадь треугольника АВС.- - -
Дано :
ΔАВС ~ ΔMNK.
∠А = ∠М.
ВС = 8.
NK = 2.
S(ΔMNK) = 12 (ед²).
Найти :
S(ΔABC) = ?
В подобных треугольниках против равных углов лежат сходственные стороны.
Отсюда стороны ВС и NK - сходственные.
Отношение сходственных сторон равно коэффициенту подобия.
То есть -
Но заметить, ища коэффициент подобия, я ставила в числитель элемент бóльшего треугольника. Поэтому при дальнейших расчётах, я буду также ставить элементы/площадь бóльшего треугольника в числитель.
Площади подобных треугольников относятся как квадрат коэффициента подобия.
В треугольнике параллельный одной из сторон треугольника отрезок, пересекающий две другие стороны треугольника в точках, отсекает от данного треугольника подобный треугольник.
Отсюда -
ΔАВС ~ ΔMBK.
В подобных треугольниках против равных углов лежат сходственные стороны. И их же отношение равно коэффициенту подобия.
∠В - общий для ΔАВС и ΔMBK.
Отсюда стороны МК и АС - сходственные.
Тогда -
Периметры подобных треугольников относятся как коэффициент подобия.
Дано :
ΔАВС ~ ΔMNK.
∠А = ∠М.
ВС = 8.
NK = 2.
S(ΔMNK) = 12 (ед²).
Найти :
S(ΔABC) = ?
В подобных треугольниках против равных углов лежат сходственные стороны.Отсюда стороны ВС и NK - сходственные.
Отношение сходственных сторон равно коэффициенту подобия.То есть -
Но заметить, ища коэффициент подобия, я ставила в числитель элемент бóльшего треугольника. Поэтому при дальнейших расчётах, я буду также ставить элементы/площадь бóльшего треугольника в числитель.
Площади подобных треугольников относятся как квадрат коэффициента подобия.Отсюда -
192 (ед²).
- - -2. В треугольнике АВС отрезок MК (М ∈ АВ, К ∈ ВС) параллелен АС. МК = 14, АС = 42. Периметр треугольника МВК равен 32. Найдите периметр треугольника АВС.- - -Дано :
ΔАВС.
М ∈ АВ, К ∈ ВС.
МК ║АС.
МК = 14.
АС = 42.
Р(ΔМВК) = 32.
Найти :
Р(ΔАВС) = ?
В треугольнике параллельный одной из сторон треугольника отрезок, пересекающий две другие стороны треугольника в точках, отсекает от данного треугольника подобный треугольник.Отсюда -
ΔАВС ~ ΔMBK.
В подобных треугольниках против равных углов лежат сходственные стороны. И их же отношение равно коэффициенту подобия.∠В - общий для ΔАВС и ΔMBK.
Отсюда стороны МК и АС - сходственные.
Тогда -
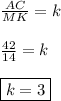
Периметры подобных треугольников относятся как коэффициент подобия.Отсюда -
96.
1. Здесь образуются два подобных (по трем углам) треугольника (большой и малый). Для них можно записать соотношение:
1,7/4 = х/8+4
откуда
х = 1,7/4 * 12 = 3 * 1,7 = 5,1
ответ: 5,1
2. 0,5 * 4=2 метра
3.Перерисуем данный рисунок в виде треугольников и обозначим интересующие нас точки.
Рассмотрим треугольники ABC и DCE.
Эти треугольники подобны, т.к.:
∠C - общий,
∠B и ∠DEC - прямые,
углы A и EDC - равны, так как являются соответственными.
Из подобия этих треугольников следует, что:
AB/DE=BC/EC
BC=(AB*EC)/DE=(9*1)/2=4,5.
В задаче нас интересует отрезок BE, BE=BC-EC=4,5-1=3,5.
ответ: 3,5