Закончи предложения соответствующей информацией о треугольниках.
1. Сумма углов треугольника KTC равна градусов.
2. Отрезок TF — это треугольника KTC, она делит треугольник на два треугольника.
3. Сумма углов ∡TKF и ∡KTF равна градусов.
4. В треугольнике KTF углу ∡KTF противолежащий катет (возможно несколько правильных ответов):
FK
KF
FT
TF
5. В треугольнике CTF углу ∡CTF прилежащий катет (возможно несколько правильных ответов):
FT
TF
FK
Объяснение:
3) По теореме Пифагора
АВ²=АС²+СВ²
АВ²=35²+12²
АВ=√(1225+144)=√1369
АВ=37 см
Квадрат катета =произведению гипотенузы на проекцию этого катета
СВ²=АВ*DB
12²=37*DB
DB=144÷37=3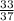
,AD=37-3
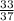=33
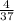
Квадрат высоты = произведению проекций этих катетов
CD²=DB*AD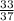=3
*33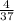
=
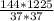, CD=√(
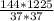)=12*35/37=420/37
8)AB=2+18=20 м
Квадрат высоты = произведению проекций этих катетов
CD²=AD*DB=2*18=36
CD=6 м
Квадрат катета =произведению гипотенузы на проекцию этого катета
AC²=AD*AB, АС=√(2*20)=2√10
По т. Пифагора
АВ²=АС²+АВ², СВ²=АВ²-АС²
СВ²=20²-(2√10)² , СВ=√(400-40)=√360=6√10
Объяснение:
3) По теореме Пифагора
АВ²=АС²+СВ²
АВ²=35²+12²
АВ=√(1225+144)=√1369
АВ=37 см
Квадрат катета =произведению гипотенузы на проекцию этого катета
СВ²=АВ*DB
12²=37*DB
DB=144÷37=3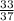
,AD=37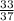-3
=33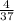
Квадрат высоты = произведению проекций этих катетов
CD²=DB*AD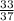=3
*33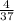
=
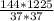, CD=√(
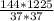)=12*35/37=420/37
8)AB=2+18=20 м
Квадрат высоты = произведению проекций этих катетов
CD²=AD*DB=2*18=36
CD=6 м
Квадрат катета =произведению гипотенузы на проекцию этого катета
AC²=AD*AB, АС=√(2*20)=2√10
По т. Пифагора
АВ²=АС²+АВ², СВ²=АВ²-АС²
СВ²=20²-(2√10)² , СВ=√(400-40)=√360=6√10