Запишите оканчания предложения 1) средней линией треугольник, называют... 2) средняя линия треугольника, соединяющая середины двух его сторон, параллельна... 3) средняя линия треугольника, соединяющая середины двух его сторон, равна...
Объяснение: зная высоту и площадь основания конуса сразу можно найти его объем по формуле: V=⅓×Sосн×h=
=⅓×36π×6=72π(см³)
Найдём радиус окружности, используя формулу обратную формуле площади:
Sосн=πr²
r²=36π÷π=36; r=√36=6см
Радиус и высота конуса образуют прямоугольный треугольник в котором радиус и высота являются катетами а образующая гипотенузой. Этот треугольник равнобедренный, поскольку высота и радиус равны 6см, а в таком треугольнике гипотенуза будет больше катета в √2 больше. Поэтому образующая L=6√2см
Теперь найдём площадь боковой поверхности конуса по формуле:
S=πrL=π×6×6√2=36π√2(см²)
Теперь найдём площадь полной поверхности конуса, зная площадь боковой поверхности и площадь основания:
Обозначим пирамиду SABCD, В правильной четырехугольной пирамиде основание – квадрат, боковые ребра равны, вершина проецируется в центр основания, т.е. в точку пересечения его диагоналей. Площадь квадрата по одной из формул равна половине произведения его диагоналей. S=d²/2.
Ребро и высота пирамиды образуют угол ASO=30°. Высота перпендикулярна основанию, треугольник AOS, образованный ребром SA, высотой SO и половиной диагонали АО – прямоугольный. АО=SO•tg30° ⇒ 0,5d=5•1/√3, d=10/√3, S=0,5•(10/√3)²= ед. площади.
ответ: V=72π(см³); Sпол=271,296см²
Объяснение: зная высоту и площадь основания конуса сразу можно найти его объем по формуле: V=⅓×Sосн×h=
=⅓×36π×6=72π(см³)
Найдём радиус окружности, используя формулу обратную формуле площади:
Sосн=πr²
r²=36π÷π=36; r=√36=6см
Радиус и высота конуса образуют прямоугольный треугольник в котором радиус и высота являются катетами а образующая гипотенузой. Этот треугольник равнобедренный, поскольку высота и радиус равны 6см, а в таком треугольнике гипотенуза будет больше катета в √2 больше. Поэтому образующая L=6√2см
Теперь найдём площадь боковой поверхности конуса по формуле:
S=πrL=π×6×6√2=36π√2(см²)
Теперь найдём площадь полной поверхности конуса, зная площадь боковой поверхности и площадь основания:
Sпол=Sосн+Sбок.пов=36π+36π√2=
=36×3,14+36×3,14×1,4=271,296см²
Обозначим пирамиду SABCD, В правильной четырехугольной пирамиде основание – квадрат, боковые ребра равны, вершина проецируется в центр основания, т.е. в точку пересечения его диагоналей. Площадь квадрата по одной из формул равна половине произведения его диагоналей. S=d²/2.
Ребро и высота пирамиды образуют угол ASO=30°. Высота перпендикулярна основанию, треугольник AOS, образованный ребром SA, высотой SO и половиной диагонали АО – прямоугольный. АО=SO•tg30° ⇒ 0,5d=5•1/√3, d=10/√3, S=0,5•(10/√3)²=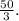
ед. площади.