Завдання 1. Із точки до площини проведено перпендикуляр і похилу, що відповідно дорівнюють: 9см і 15см. Знайти: довжину проекції похилої; величину кута між похилою та площиною.
∠А=180°-(90°+60°)=180°-150°=30°-по теореме о сумме углов в треугольнике.
В условии сказано что сумма гипотенузы и меньшего катета равна 30 см. Чтобы понять какой катет меньший, для это нужно посмотреть на углы, которые находятся напротив катетов. Напротив ∠А находится самый маленький катет, т.к ∠А самый маленький в этом треугольнике.
Значит, СВ+АВ=30 см.
Напротив угла равного 30° лежит катет СВ⇒ он равен половине гипотенузы АВ.
ответ: Ѕ=640 см²
Объяснение:
Пусть М - середина ВС, ВН - перпендикуляр из В на АС.
В прямоугольном ∆ FMC из Пифагоровых троек 8:15:17 ( или по т.Пифагора) катет МF=8 (см).
MF - средняя линия ∆ НВС⇒ в ∆ АВС высота ВН =2•MF=16 (СМ)
Одна из формул площади треугольника
S=0,5•h•а (h- высота, а - сторона, к которой она проведена)
S(ABC)=0,5•16•(25+15)=640 (см²)
или по другой формуле:
S=0,5•a•b•sinα, где а и b - стороны треугольника, α - угол между ними.
sin∠MCA=MF:MC=8/17
S (АВС)=0,5•40•34•8/17=640 (см²)
10 см.
Объяснение:
✓РЕШЕНО МУДROST✓
Если ∠С = 90°, а ∠В=60°, то
∠А=180°-(90°+60°)=180°-150°=30°-по теореме о сумме углов в треугольнике.
В условии сказано что сумма гипотенузы и меньшего катета равна 30 см. Чтобы понять какой катет меньший, для это нужно посмотреть на углы, которые находятся напротив катетов. Напротив ∠А находится самый маленький катет, т.к ∠А самый маленький в этом треугольнике.
Значит, СВ+АВ=30 см.
Напротив угла равного 30° лежит катет СВ⇒ он равен половине гипотенузы АВ.
Пусть х см - гипотенуза АВ, то
СВ=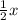
Составим и решим уравнение:
x+0,5х=30
1,5х=30
х=30:1,5
х=20
Итак: гипотенуза АВ=20 см, тогда
СВ=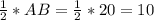 см.
см.
✓РЕШЕНО МУДROST✓