Завдання на повторення пикільного матеріалу з геометрі 1. Висота ВМ трикутника АВС ділить сторону АС на відрізки АМ і СМ так, що АМ=12см, CM 4см, LA=30°. Знайдіть: а) довжину сторони ВС; б) площу трикутника АВС; в) радіус кола, описаного навколо трикутника АВС. 2. Знайдіть площу круга, вписаного в трикутник зі сторонами 4см, 13см і 15см. 3. Один з катетів прямокутного трикутника дорівнює 30см, а радіус описаного навколо нього кола - 17см. Обчисліть площу даного трикутника. 4. 4. Бісектриса тупого кута паралелограма ділить його сторону на відрізки завдовжки 3см і 5см, рахуючи від вершини гострого кута, який дорівнює 60°. Обчисліть кути паралелограма, його периметр та площу. 5. Площа ромба дорівнює 120см", а його діагоналі відносяться як 5:12. Знайдіть периметр ромба. 6. Менша основа прямокутної трапеції дорівнює 12см, а менша бічна сторона - 4v3 см. Знайдіть площу трапеції, якщо один із ї кутів дорівнює 120°. 7. Менша основа рівнобічної трапеції порівнює 15см, а висота - 3v3 см. Знайдіть бічну сторону та площу трапецӣ, якщо один із ії кутів дорівнює 150°. Задание на повторение пикильного материала по геометре 1. Высота ВМ треугольника АВС делит сторону АС на отрезки АМ и СМ так, что АМ=12см, CM 4см, LA=30°. Найдите: а) длину стороны ВС; б) площадь треугольника АВС; в) радиус круга, описанного вокруг треугольника АВС. 2. Найдите площадь круга, вписанного в треугольник со сторонами 4см, 13см и 15см. 3. Один из катетов прямоугольного треугольника равен 30см, а радиус описанного вокруг него кола-17см. Вычислите площадь данного треугольника. 4. 4. Биссектриса тупого угла параллелограмма делит его сторону на отрезки длиной 3см и 5см, считая от вершины острого угла, который равен 60°. Вычислите углы параллелограмма, его периметр и площадь. 5. Площадь ромба равна 120см", а его диагонали относятся как 5:12. Найдите периметр ромба. 6. Меньшее основание прямоугольной трапеции равна 12см, а меньшая боковая сторона - 4v3 см. Найдите площадь трапеции, если один из ее углов равен 120°. 7. Меньшая основа рівнобічної трапеции сравнивает 15см, а высота - 3v3 см. Найдите боковую сторону и площадь трапецӣ, если один из ее углов равен 150°.
Один из сторон — перпендкулярен прямой, тоесть эта же сторона образует 2 прямых угла, тоесть, треугольник — прямоугольный.
Наклонная(или гипотенуза) — равна 12 сантиметров, и с прямой она образует угол 30-и градусов.
Теорема о 30-градусном угле прямоугольного треугольника такова: катет, противолежащий углу 30-градусов в прямоугольном треугольнике — равен половине гипотенузы
А перпендикуляр лежит на против этого же угла 30-градусов, тоесть — прерпендикуляр равен половине наклонной, тоесть перпендикуляр равен: 12/2 = 6.
Теперь мы знаем гипотенузу, и один и катетов, чтобы найти проекцию(второй катет) — используем теорему Пифагора: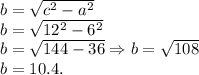
Вывод: перпендикуляр равен — 6 см; проекция равна — 10.4см(или √108, как удобнее).
Объяснение:
Пусть с точки С опустили две наклонние на плоскость, в пересечении получили точки А и в
В результате имеем ДАВС, где /_С=90°
Опустим перпендикуляр с точки с на плоскость, получим точку Н Известно, что /_CAH=45° и /_СВН=30°, СВ=
Тогда из ДСНB /_H=90°, /_B=30°и CB=8 имеем
СН=4, как катет против угла 30°
Из ДСНА, где /_H=90° и /_A=45° следует, что и /_НСА=45° → ДСНА равнобедренний CH=HA=4
По теореме Пифагора СА=4√2
Из ∆АВС: /_C=90°, из условия, СВ=8,
CA=4√2
За теоремою Пифагора
ВА^2=СВ^2+СА^2=64+32=96
BA=4√6