Формула линейной функции имеет вид y=kx+b, где х — независимая переменная (абсцисса точки); y — зависимая переменная (ордината точки); k, b — числовые коэффициенты.
Числовой коэффициент b показывает, в какой точке график пересекает ось ординат (Оу). В данном случае b = 3. Наша формула обретет вид:
Числовой коэффициент k отвечает за наклон графика линейной ф-ции:
Если график ф-ции образует с положительной осью Ox острый угол, тогда коэффициент k > 0, если тупой — k < 0.
В данном случае k < 0, то есть k — отрицательное число.
Из формулы выразим k:
Возьмём любую удобную нам точку на прямой и подставим ее координаты в полученную формулу:
A (4; 0)
В итоге, формула линейной функции получится следующей:
Объяснение: для нахождения площади трапеции нам не известна ее высота. Известно, что угол между основанием и боковой стороной образует угол 30°. При проведении высоты образуется прямоугольный треугольник с гипотенузой 8 см и катетом, лежащим против угла 30°. Этот катет и будет высотой трапеции. Найдем высоту трапеции, она будет равна половине гипотенузы, т.е. 10:2=5 см. Теперь найдем площадь трапеции: она равна половине суммы оснований умноженных на высоту: (8+12):2х5=50см²
Формула линейной функции имеет вид y=kx+b, где х — независимая переменная (абсцисса точки); y — зависимая переменная (ордината точки); k, b — числовые коэффициенты.
Числовой коэффициент b показывает, в какой точке график пересекает ось ординат (Оу). В данном случае b = 3. Наша формула обретет вид:
Числовой коэффициент k отвечает за наклон графика линейной ф-ции:
Если график ф-ции образует с положительной осью Ox острый угол, тогда коэффициент k > 0, если тупой — k < 0.
В данном случае k < 0, то есть k — отрицательное число.
Из формулы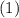
выразим k:
Возьмём любую удобную нам точку на прямой и подставим ее координаты в полученную формулу:
A (4; 0)В итоге, формула линейной функции получится следующей:
ответ: площадь трапеции 50 см²
Объяснение: для нахождения площади трапеции нам не известна ее высота. Известно, что угол между основанием и боковой стороной образует угол 30°. При проведении высоты образуется прямоугольный треугольник с гипотенузой 8 см и катетом, лежащим против угла 30°. Этот катет и будет высотой трапеции. Найдем высоту трапеции, она будет равна половине гипотенузы, т.е. 10:2=5 см. Теперь найдем площадь трапеции: она равна половине суммы оснований умноженных на высоту: (8+12):2х5=50см²