В равнобедренном треугольнике медиана, проведённая к основанию, является биссектрисой и высотой . Дано: DABC - равнобедренный; AB - основание. CD - медиана .
Док-ть: CD - высота и биссектриса .
Доказательство:
CA=CD - по условию РA= РB - по свойству равнобедренного треугольника AD=DB т. к. CD - медиана , ЮDCAD=DCBD (по 1-ому признаку равенства треугольников) ЮРACD= РBCD, РADC= РBDC РACD=РBCD Ю CD - биссектриса РACD и РBCD - смежные и равны Ю РACD и РBCD - прямые Ю CD - высота треугольника. ещё доказательство: http://oldskola1.narod.ru/Nikitin/0018.htm
AM - медиана треугольника ABC, то BE = EC = BC/2 = AE/2.
Сделаем дополнительное построение, т.е. построим до параллелограмма ABDC, в нём AD = 2AE = 2BC, тогда сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон:
Не трудно заметить, что треугольник ABC - прямоугольный с гипотенузой AB = √7 и катетами AC = √3; BC = 2.
2) Площадь треугольника: кв. ед.
3) Центр описанной окружности лежит на середине гипотенузы, значит радиус описанной окружности равен половине гипотенузы.
Дано:
DABC - равнобедренный;
AB - основание. CD - медиана .
Док-ть:
CD - высота и биссектриса .
Доказательство:
CA=CD - по условию
РA= РB - по свойству равнобедренного треугольника
AD=DB т. к. CD - медиана ,
ЮDCAD=DCBD (по 1-ому признаку равенства треугольников)
ЮРACD= РBCD, РADC= РBDC
РACD=РBCD Ю CD - биссектриса
РACD и РBCD - смежные и равны
Ю РACD и РBCD - прямые Ю CD - высота треугольника. ещё доказательство: http://oldskola1.narod.ru/Nikitin/0018.htm
Пусть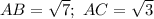 . Из условия AE = BC, а так как
. Из условия AE = BC, а так как
AM - медиана треугольника ABC, то BE = EC = BC/2 = AE/2.
Сделаем дополнительное построение, т.е. построим до параллелограмма ABDC, в нём AD = 2AE = 2BC, тогда сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон:
Не трудно заметить, что треугольник ABC - прямоугольный с гипотенузой AB = √7 и катетами AC = √3; BC = 2.
2) Площадь треугольника: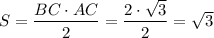 кв. ед.
кв. ед.
3) Центр описанной окружности лежит на середине гипотенузы, значит радиус описанной окружности равен половине гипотенузы.