1. Площади подобных треугольников относятся как квадрат коэффициента подобия.
Т.к. стороны A₁ B₁ C₁ в 2 раза меньше сторон ABC, то коэффициент подобия равен 2, =>
(см²)
2) Пусть сторона большого куба равна , тогда по условию сторона меньшего куба равна .
Объем большого куба: (см³)
Объем меньшего куба: (см³)
3) Матрешку можно рассматривать как цилиндр.
Формула массы цилиндра: - плотность материала, - объем цилиндра.
Формула объема цилиндра: - радиус основания, - высота цилиндра.
Если меньшая матрешка вдвое меньше большей, то делаем вывод что высота большей матрешки вдвое больше высоты меньшей матрешки, а также радиус основания большей матрешки вдвое больше радиуса основания меньшей матрешки.
Пусть - радиус основания меньшей матрешки, - высота меньшей матрешки, тогда по формуле:
1) 25
2) 15,625
3)1,2
Объяснение:
1. Площади подобных треугольников относятся как квадрат коэффициента подобия.
Т.к. стороны A₁ B₁ C₁ в 2 раза меньше сторон ABC, то коэффициент подобия равен 2, =>
2) Пусть сторона большого куба равна , тогда по условию сторона меньшего куба равна
, тогда по условию сторона меньшего куба равна 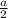 .
.
Объем большого куба: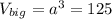 (см³)
(см³)
Объем меньшего куба: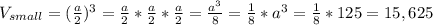 (см³)
(см³)
3) Матрешку можно рассматривать как цилиндр.
Формула массы цилиндра: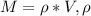 - плотность материала,
- плотность материала, 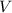 - объем цилиндра.
- объем цилиндра.
Формула объема цилиндра: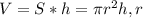 - радиус основания,
- радиус основания, 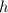 - высота цилиндра.
- высота цилиндра.
Если меньшая матрешка вдвое меньше большей, то делаем вывод что высота большей матрешки вдвое больше высоты меньшей матрешки, а также радиус основания большей матрешки вдвое больше радиуса основания меньшей матрешки.
Пусть - радиус основания меньшей матрешки,
- радиус основания меньшей матрешки, 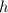 - высота меньшей матрешки, тогда по формуле:
- высота меньшей матрешки, тогда по формуле:
Объяснение:
1.Найти площадь поверхности и объем конуса, если образующая равна 10см ,радиус основания-6см.
S(конуса)=πrl +πr² ,V(конуса)=1/3*πr²*h
S(конуса)=π*6*10 +π*6²=96π,
Комбинация радиуса , образующей и высоты конуса образует прямоугольный треугольник с гипотенузой 10 .Поэтому по т Пифагора h=√(100-36)=8
V(конуса)=1/3*π*6²*8=96 π .
2.Найти площадь поверхности и объем цилиндра, если высота цилиндра равна 22,5см,радиус основания-12см.
S(цилиндра)=2πr²+2πr²h , V(цилиндра)=πr²*h .
S(цилиндра)=2π*12²+2π*12²*22,5=144* 2π(1+22,5)=3384 π,
V(цилиндра)=π*12²*22,5=3240 π .
3.Найти площадь поверхности и объем шара, радиус шара-9см.
S(шара)=4πr² , V(шара)=4/3*πr³
S(шара)=4π*9²=324π , V(шара)=4/3*π*9³=972π