2. Высота поделила основу пополам,тем самым поделив треугольник на 2 маленьких.По теореме Пифагора квадрат гипотенузы = сумме квадратов катетов. Найдём катет( половину основы треугольника).
225 = 81 +
= 225 - 81 = 144
х = = 12 см
Теперь узнаем длинну основы: 12 +12 = 24 см
3.Площадь ромба через его сторону и угол
S = a²·sin(β) = (7√2)²·sin(135°) = 49*2 * 1/√2 = 49√2 см
4. Не знаю, прости((((
5.Дано: трапеція КМРТ, МР=7 см, КТ=9 см, ∠Т=45°.
Проведемо висоту РН. Розглянемо ΔРТН - прямокутний.
∠Т=45°, тоді ∠ТРН=90-45=45°, тобто ΔРТН - рівнобедрений.
ответ:Номер 1
180-(40+60)=80 градусов
Номер 2
Продолжаешь сторону КМ и получается внешний угол
Номер 3
Углы при основании равнобедренного треугольника равны
<1=120 градусов
<2=<3=(180-120):2=30 градусов
Номер 4
Высота-это перпендикуляр,она образовала при соприкосновении с основанием два прямых угла
<FAM=<FAP=90 градусов
<М=180-(20+90)=70 градусов
<Р=180-(70+20+80)=10 градусов
Проверка
180-(80+90)=10 градусов
Номер 6
Сумма двух внутренних углов не смежных с внешним равна градусной мере внешнего угла
<1=Х
<2=Х-20
Х+Х-20=140
2Х=140+20
Х=160:2
Х=80
<1=80 градусов
<2=80-20=60 градусов
Сумма внешнего и смежного ему внутреннего угла равна 180 градусов
<3=180-140=40 градусов
Номер 7
Рассмотрим треугольник АСВ
<А=180-(90+60)=30 градусов
Рассмотрим треугольник DCB
Если DC=CB,то образовавшийся треугольник прямоугольный равнобедренный и углы при его основании равны между собой и равны
<СDB=<CBD=90:2=45 градусов
<DBA=<B-<CBD=60-45=15 градусов
<ВDA=180-(30+15)=135 градусов
Объяснение:
1. 12 * 7 = 84 см"
2. 24 см
3.49√2 см
4. -----------
5.24√2 см²
Объяснение:
1. Тут и так понятно)
2. Высота поделила основу пополам,тем самым поделив треугольник на 2 маленьких.По теореме Пифагора квадрат гипотенузы = сумме квадратов катетов. Найдём катет( половину основы треугольника).
225 = 81 +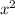
х =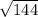
= 12 см
Теперь узнаем длинну основы: 12 +12 = 24 см
3.Площадь ромба через его сторону и угол
S = a²·sin(β) = (7√2)²·sin(135°) = 49*2 * 1/√2 = 49√2 см
4. Не знаю, прости((((
5.Дано: трапеція КМРТ, МР=7 см, КТ=9 см, ∠Т=45°.
Проведемо висоту РН. Розглянемо ΔРТН - прямокутний.
∠Т=45°, тоді ∠ТРН=90-45=45°, тобто ΔРТН - рівнобедрений.
Нехай РН=ТН=х см, тоді за теоремою Піфагора
х²+х²=6²; 2х²=36; х²=18; х=√18=3√2; РН=3√2 см.
S=(МР+КТ):2*3√2=(7+9)/2*3√2=24√2 см²