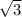Возьмем точки А и В так, чтобы XKNA и XLMB были параллелограммами и продлим XY за точку Y на свою длину до точки С (см. рис). Треугольник ANY равен треугольнику BMY по двум сторонам и углу между ними (AN=XK=XL=BM, NY=MY и ∠ANY=∠BMY как внутренние накрест лежащие, т.к. АN||KL||MB и MN - секущая). Значит AY=BY, т.е. AXBC - параллелограмм. Тогда ∠KVX=∠AXY=∠XCB, ∠LWX=∠BXC, BC=XA=KN и BX=LM, а т.к. по условию LM<KN, то BX<BС. Т.к. в любом треугольнике (в том числе XCB) напротив меньшей стороны лежит меньший угол, то ∠XCB<∠BXC, а значит и ∠KVX<∠LWX.
Объяснение: так там угол в 60 а сумма дополнительных углов 180 то соседний равен <CDA= 120 и так это ромб <ВAD=60 градусам так как диагональ BD делит углы B и D пополам а так же делит на два равносторонних треугольника BAD и BCD то диагональ BD равна 8 , теперь вычислим площадь ромба по формуле ab*sinL так как стороны равны sinL не важно какой угол мы возьмем sin120 или sin 60 они равны но если вы не формулу суммы углов то лучше использовать sin60 и мы вычисляем *sin60= *64= 32
ответ:32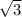
Объяснение: так там угол в 60 а сумма дополнительных углов 180 то соседний равен <CDA= 120 и так это ромб <ВAD=60 градусам так как диагональ BD делит углы B и D пополам а так же делит на два равносторонних треугольника BAD и BCD то диагональ BD равна 8 , теперь вычислим площадь ромба по формуле ab*sinL так как стороны равны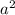
sinL не важно какой угол мы возьмем sin120 или sin 60 они равны но если вы не формулу суммы углов то лучше использовать sin60 и мы вычисляем 
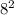*sin60= 
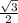*64= 32