1.Если в четырехугольник вписана окружность и две стороны равны, то и другие две тоже равны. ( доказывается так же как доказывается теорема о том что если в четырехугольник можно вписать окружность, то суммы противолежащих сторон равны)
2. АСперпендикулярна ВД.( треугольники адс и абс равны по трем сторонам - значит ас - биссектриса, а т.к треугольник АВД равнобедренный, то высота и медиана) отсюда
3 ВД точкой пересечения делится пополам. обозначим ее О. ВО=Од=6
Вспомним формулу площади четырехугольника - половина произведения диагоналей на синус угла между ними, а , т.к диагонали перпендикулярны, то половине произведения диагоналей, т.еSавсд= АС*ВД/2=42.
4. Площадь четырехугольника равна - произведению полупериметра на радиус вписанной окружности, т.е.(P/2)*r. (P/2)*3=42, (P/2)=14, P=28
5. АО=х, ОС=(7-х)
6. По теореме пифагора находим АВ и ВС и помним, что их сумма равна полупериметру.
Переносим один из корней в левую часть, возводим в квадрат, уничтожаются уничтожаются. еще раз разделяем на две стороны и возводим в квадрат
уменя получилось уравнение
х=2,5 или х=4.5
находим площадь, учитывая. что диагонали взаимно перпендикулярны
1.Если в четырехугольник вписана окружность и две стороны равны, то и другие две тоже равны. ( доказывается так же как доказывается теорема о том что если в четырехугольник можно вписать окружность, то суммы противолежащих сторон равны)
2. АСперпендикулярна ВД.( треугольники адс и абс равны по трем сторонам - значит ас - биссектриса, а т.к треугольник АВД равнобедренный, то высота и медиана) отсюда
3 ВД точкой пересечения делится пополам. обозначим ее О. ВО=Од=6
Вспомним формулу площади четырехугольника - половина произведения диагоналей на синус угла между ними, а , т.к диагонали перпендикулярны, то половине произведения диагоналей, т.еSавсд= АС*ВД/2=42.
4. Площадь четырехугольника равна - произведению полупериметра на радиус вписанной окружности, т.е.(P/2)*r. (P/2)*3=42, (P/2)=14, P=28
5. АО=х, ОС=(7-х)
6. По теореме пифагора находим АВ и ВС и помним, что их сумма равна полупериметру.
Переносим один из корней в левую часть, возводим в квадрат,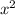
уничтожаются 
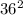уничтожаются. еще раз разделяем на две стороны и возводим в квадрат
уменя получилось уравнение
х=2,5 или х=4.5
находим площадь, учитывая. что диагонали взаимно перпендикулярны
12*2,5)/2=15 или (12+4,5)/2=27.
проверьте вычисленпия, могла ошибиться.
искомое сечение - симметричный четырехугольник BPKL
диагонали PL , BK пересекаются под углом 90 град
по условию
стороны основания AB=BC=CD=AD =3
боковые ребра MA=MB=MC=MD =8
точка К - середина ребра MD ; KD = MD /2 = 8/2=4
ABCD -квадрат
диагональ AC = BD = 3√2
пересечение диагоналей точка F : BF =FD = BD/2 =3√2 /2 =1.5√2
BK - медиана треугольника MBD
длина медианы BK = 1/2 √(2 BM^2 +2 BD^2 - MD^2 ) =1/2 √(2*8^2 +2*(3√2)^2 - 8^2 ) =5
по теореме косинусов
cos KBD = ( KD^2 - (BK^2+BD^2) )/ (-2*BK*BD)= ( 4^2 - (5^2+(3√2)^2) )/ (-2*5*3√2)= 9/(10√2)
MF - высота
треугольник EBF - прямоугольный
BE = BF / cos KBD = 1.5√2 / [ 9/(10√2)] = 10/3
по теореме Пифагора EF =√(BE^2 - BF^2) =√( (10/3)^2 - (1.5√2)^2) =√238/6
MF - высота
треугольник MFB - прямоугольный
по теореме Пифагора MF =√( MB^2 -BF^2) =√( 8^2- (1.5√2)^2 ) =√238/2
ME =MF -EF =√238/2- √238/6= √238/3
треугольники MPL ~ MCA подобные
PL / AC = ME /MF ; PL = AC * ME /MF = 3√2 * √238/3 /√238/2 =2√2
площадь сечения(четырехугольника BPKL)
Sс = PL*BK *sin<BEP /2 = 2√2*5*sin90 /2 = 5√2
ответ 5√2