Проводим прямую a и ставив НАД ней точку К Далее берем циркуль, раскрываем до такого радиуса, что при приложении его к точке К он выходил за предел прямой.
После ставим острие циркуля к точке и проводим окружность (можно как на рисунке) НЕ МЕНЯЕМ РАЗМЕР и проводим окружности в точках пересечениях.
Эти окружности должны пересечься. Соединяем их и получаем перпендикуляр.
Теперь биссектриса. Ставим острие циркуля в точку и проводим небольшую окружность (полуокружность) НЕ МЕНЯЕМ РАЗМЕР и ставим острие в точки пересечения. Проводим окружности и получаем точку. Соединяем ее и точку угла. Получаем биссектрису.
Дана трапеция ABCD, BC║AD, AB=CD, BC=8см, AD=14см, S(ABCD)=44см².
Найти P(ABCD).
Пусть CM⊥AD, BN⊥AD и M,N∈AD.
Площадь трапеции равна произведению средней линии и высоты опущенной на основание.
S(ABCD) =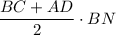
= BN·(8см+14см):2 = BN·11см = 44см²
BN = 44:11 см = 4см
ΔABN = ΔDCM по гипотенузе и острому углу (AB=DC и ∠BAN=∠CDM т.к. трапеция равнобедренная), поэтому AN=MD
NBCM - прямоугольник, поэтому NM=BC=8см
AN = (AD-NM):2 = (14см-8см):2 = 3см
В прямоугольном ΔABN (∠N=90°): BN=4см и AN=3см, по Египетскому треугольнику AB=5см.
CD=AB=5см
P(ABCD) = AB+BC+CD+AD = 5см+8см+5см+14см = 32см
ответ: 32см.
Проводим прямую a и ставив НАД ней точку К
Далее берем циркуль, раскрываем до такого радиуса, что при приложении его к точке К он выходил за предел прямой.
После ставим острие циркуля к точке и проводим окружность (можно как на рисунке)
НЕ МЕНЯЕМ РАЗМЕР и проводим окружности в точках пересечениях.
Эти окружности должны пересечься. Соединяем их и получаем перпендикуляр.
Теперь биссектриса.
Ставим острие циркуля в точку и проводим небольшую окружность (полуокружность)
НЕ МЕНЯЕМ РАЗМЕР и ставим острие в точки пересечения. Проводим окружности и получаем точку. Соединяем ее и точку угла. Получаем биссектрису.
Все.~