Знайдить площу повной поверхни правельной чотирекутной пирамиди кожне ребро якой доривнюе альфа

Чертежи смотрите во вложении.

✧Задание №1.✧

В прямоугольном равнобедренном треугольнике гипотенуза равна 12 см. Найти катеты этого треугольника.

Дано :

ΔАВС - равнобедренный и прямоугольный (∠В = 90°, АВ = СВ).

АС = 12 см.

Найти :

АВ = ?

СВ = ?

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы (теорема Пифагора).

Пусть АВ = СВ = х. Тогда АВ² + СВ² = АС²

х² + х² = 12²

2х² = 144

х² = 72

х₁ =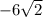 - не удовлетворяет условию задачи, так как длины отрезков не могут выражаться отрицательными числами.

х₂ =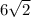 - подходит.

Тогда АВ = СВ = х =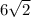 см.

см, см.

✧Задание №2.✧

Найти меньшую диагональ ромба, если его сторона равна 13 см, а большая диагональ ромба равна 24 см.

Дано :

Четырёхугольник ABCD - ромб.

ВС = 13 см, АС = 24 см.

Найти :

BD = ?

В ромбе диагонали точкой пересечения делятся пополам и взаимно перпендикулярны.

Следовательно, АС⊥BD, ВО =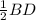 , CO = 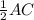= 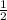*24 см = 12 см.

Рассмотрим ΔВОС - прямоугольный (∠ВОС = 90°).

По теореме Пифагора -

ВО² + СО² = ВС²

ВО² = ВС² - СО² = 13² - 12² = 169 - 144 = 25 ⇒ ВО =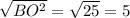 см.

Тогда BD = 2*BO = 2*5 см = 10 см.

10 см.

Обозначим точку пересечения высот  треугольника - М,
основание высоты из С на АВ Н, из В на АС - К.  
Рассмотрим треугольники ВМН и СМК.
Они прямоугольные по построению и имеют равные острые углы ( вертикальные при М- точке пересечения высот).
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Следовательно, вписанные ∠ С1СА=∠В1ВА и  дуги, на которые они опираются, также равны. 
⇒ дуга С1АВ1, равная 180°,  делится точкой А на две равные дуги по 90°.
Вписанный угол АСС1 опирается на дугу 90°и равен половине ее градусной меры.
∠АСС1=45°
Треугольник СНА - прямоугольный. Сумма острых углов прямоугольного треугольника равна 90°.
Угол НАС=90°- 45°=45°
ответ: угол ВАС=45°
[email protected]