Опусти перпендикуляр из вершины С на АД: СМ ⊥ АД .
Тогда ВСМН - прямоугольник , противоположные стороны которого равны, ВС=МН и ВН=СМ , но так как по условию ВС=ВН, то ВСМН - квадрат, сторону которого обозначим "а" .
ΔАВН - прямоугольный, с углом ∠А=45° . Тогда и ∠АВН=90°-45°=45° .
Извини наверно опечатки в условии 1. Сумма углов треугольника 180. 180-90-45=45 Значит треугольник равносторонний и его катеты равны. Биссектриса в равностороннем треугольнике делит сторону и угол пополам и образует два новых равносторонних треугольника со сторонами равными 4 АД =4 АВ=8 В остальных задачах свойства углов и биссектрисы, то, что против угла в 30 градусов лежит сторона равная половине гипотенузы г). в треугольнике треугольник АВД равносторонний углы равны 45 градусов - значит и стороны равны и равны 5 АД=5 см ДС лежит против угла в 30 - значит равна половине вс или 7/2 = 3.5 АС=5+3.5= 8.5
ответ: h=5 см .
АВСД - трапеция, АВ=СД , ∠А=∠Д=45° ,
ВС=а , ВН ⊥ АД , h=ВН=ВС=а , S(трап)=50см² .
Опусти перпендикуляр из вершины С на АД: СМ ⊥ АД .
Тогда ВСМН - прямоугольник , противоположные стороны которого равны, ВС=МН и ВН=СМ , но так как по условию ВС=ВН, то ВСМН - квадрат, сторону которого обозначим "а" .
ΔАВН - прямоугольный, с углом ∠А=45° . Тогда и ∠АВН=90°-45°=45° .
То есть ΔАВН - равнобедренный и АН=ВН=а .
Аналогично, из ΔСДМ получаем, что ДМ=СМ=а .
Тогда АД=АН+НМ+МД=а+а+а=3а .
Площадь трапеции :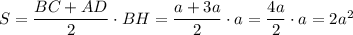
По условию: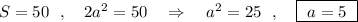
1. Сумма углов треугольника 180. 180-90-45=45 Значит треугольник равносторонний и его катеты равны. Биссектриса в равностороннем треугольнике делит сторону и угол пополам и образует два новых равносторонних треугольника со сторонами равными 4 АД =4 АВ=8
В остальных задачах свойства углов и биссектрисы, то, что против угла в 30 градусов лежит сторона равная половине гипотенузы
г). в треугольнике треугольник АВД равносторонний углы равны 45 градусов - значит и стороны равны и равны 5 АД=5 см ДС лежит против угла в 30 - значит равна половине вс или 7/2 = 3.5 АС=5+3.5= 8.5