чтобы найти периметр параллелограмма нужно найти длины двух его сторон например АВ и ВС по формуле: АВ²=(Ах-Вх)²+(Ау-Ву)²+(Аz-Bz)²=
=(2-1)²+(1-0)²+(3-7)²=1²+1²+(-4)²=2+16=18;
AB=√18=3√2;
Точно так же найдём длину стороны ВС:
ВС²=(1-(-2))²+(0-1)²+(7-5)²=(1+2)²+1²+2²=
=3²+1+4=9+5=14; ВС=√14
СД²=(-2-(-1))²+(1-2)²+(5-1)²=(-2+1)²+(-1)²+4²=
=(-1)²+1+16=1+17=18; СД=√18=3√2;
АД²=(2-(-1))²+(1-2)²+(3-1)²=(2+1)²+(-1)²+2²=
=3²+1+4=9+5=14; АД=√14
Мы нашли все 4 стороны, но достаточно двух.
Все стороны совпадают и теперь найдём периметр параллелограмма.
Р=АВ+ВС+СД+АД=2×3√2+2×√14=
=6√2+2√14. Разные корни не прибавляются, и можно оставить так, но можно найти приблизительное значение корней и найти нужное число, округлив до десятых: √2≈1,4; √14≈3,7, получим:
6×1,4+2×3,7=8,4+7,4=15,8
ЗАДАНИЕ 2
Так как точка М- середина отрезка АВ, то её координаты найдём по формуле:
Дано:
ΔABC, ∠B = 90°.
Вписанная окружность с центром O и радиусом OD = OE = OF,
D∈BC, E∈AC, F∈AB.
OE = 12 (см), EC = 8 (см).
Найти:
Заметим, что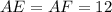 и
и  (так как отрезки касательных, проведенных к окружности из одной точки, равны).
(так как отрезки касательных, проведенных к окружности из одной точки, равны).
Пусть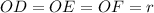 .
.
Тогда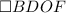 - квадрат, так как
- квадрат, так как  (и, значит,
(и, значит, 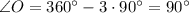 ), а также
), а также 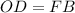 ,
,  и
и 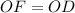 . - Все стороны и углы данного четырехугольника равны.
. - Все стороны и углы данного четырехугольника равны.
Значит,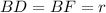 .
.
Тогда катеты треугольника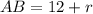 и
и 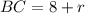 , а гипотенуза равна
, а гипотенуза равна 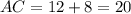 .
.
По тереме Пифагора:
Второй корень нам не подходит (он отрицательный ... ).
Так что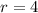 .
.
Можем найти площадь:
Задача решена!
96 см².
ответ: Р=6√2+2√14 или 15,8
Объяснение: ЗАДАНИЕ 1
чтобы найти периметр параллелограмма нужно найти длины двух его сторон например АВ и ВС по формуле: АВ²=(Ах-Вх)²+(Ау-Ву)²+(Аz-Bz)²=
=(2-1)²+(1-0)²+(3-7)²=1²+1²+(-4)²=2+16=18;
AB=√18=3√2;
Точно так же найдём длину стороны ВС:
ВС²=(1-(-2))²+(0-1)²+(7-5)²=(1+2)²+1²+2²=
=3²+1+4=9+5=14; ВС=√14
СД²=(-2-(-1))²+(1-2)²+(5-1)²=(-2+1)²+(-1)²+4²=
=(-1)²+1+16=1+17=18; СД=√18=3√2;
АД²=(2-(-1))²+(1-2)²+(3-1)²=(2+1)²+(-1)²+2²=
=3²+1+4=9+5=14; АД=√14
Мы нашли все 4 стороны, но достаточно двух.
Все стороны совпадают и теперь найдём периметр параллелограмма.
Р=АВ+ВС+СД+АД=2×3√2+2×√14=
=6√2+2√14. Разные корни не прибавляются, и можно оставить так, но можно найти приблизительное значение корней и найти нужное число, округлив до десятых: √2≈1,4; √14≈3,7, получим:
6×1,4+2×3,7=8,4+7,4=15,8
ЗАДАНИЕ 2
Так как точка М- середина отрезка АВ, то её координаты найдём по формуле:
Мх=(Ах+Вх)/2=(1+6)/2=7/2=3,5
Му=(Ау+Ву)/2=(3-5)/2= -2/2= –1
Мz=(Az+Bz)/2=(-8-10)/2= –18/2= –9
ОТВЕТ: M(3,5; -1; -9)