Угол, косинус которого имеет отрицательный знак, - тупой. Он – смежный острому углу с таким же косинусом со знаком "+".
cos(180°-α)= -cosα
Построим острый угол с положительным косинусом 5/13. Смежным ему будет тупой угол с данным в условии косинусом -5/13.
Косинус - отношение в прямоугольном треугольнике катета , прилежащего к данному углу, к гипотенузе.
Для этого построения нам надо найти второй катет прямоугольного треугольника, в котором один катет равен 5, гипотенуза - 13.
Пусть нам надо построить треугольник АВС с прямым углом С.
Известны гипотенуза АВ=13, катет АС=5
По т. Пифагора ВС²=АВ²-АС²
ВС=√(169-25)=12
Построение. На луче СМ отложим отрезок АС=5
Из точки А как из центра чертим полуокружность радиусом 13 см.
Из точки С как из центра чертим полуокружность радиусом 12 см.
Точку их пересечения обозначим В.
Соединим А и В. Косинус угла ВАС=АС:АВ=5/13.
Косинус смежного ∠ВАМ= -5/13. Это искомый угол.
Из точки С по общепринятому методу возводим перпендикуляр. На нем откладываем катет СВ=12 см.
Соединяем В и А. В построенном треугольнике косинус угла А равен 5/13. Смежный ему тупой угол ВАМ - искомый, его косинус - 5/13.
На листочке в клеточку отмечено три точки F, S, D. Известно , что площадь одной клеточки 4 см². Рассчитайте расстояние от F до SD в метрах.
Объяснение:
Расстояние это перпендикуляр. Пусть FH⊥SD. Тогда FH расстояние до SD.
Найдем длину квадрата площадью 4 см² ⇒2*2=4, значит сторона квадрата 2 см.
Пусть SК⊥FD . Найдем площадь ΔFSD
S=1/2*FD*SK , S=1/2*8*6=24 (см²).
С другой стороны S( ΔFSD)=1/2*SD*FH .Нахождение SD внизу.
24=1/2*6√2*FH ⇒FH= , FH=4√2 см=0,04√2 м
Расстояние от F до SD 0,04√2 м
==================
В желтом прямоугольном треугольнике , со стороной 6 см, по т. Пифагора, SD=√(6²+6²)=√(2*6²)=6√2 ( cм)
Угол, косинус которого имеет отрицательный знак, - тупой. Он – смежный острому углу с таким же косинусом со знаком "+".
cos(180°-α)= -cosα
Построим острый угол с положительным косинусом 5/13. Смежным ему будет тупой угол с данным в условии косинусом -5/13.
Косинус - отношение в прямоугольном треугольнике катета , прилежащего к данному углу, к гипотенузе.
Для этого построения нам надо найти второй катет прямоугольного треугольника, в котором один катет равен 5, гипотенуза - 13.
Пусть нам надо построить треугольник АВС с прямым углом С.
Известны гипотенуза АВ=13, катет АС=5
По т. Пифагора ВС²=АВ²-АС²
ВС=√(169-25)=12
Построение. На луче СМ отложим отрезок АС=5
Из точки А как из центра чертим полуокружность радиусом 13 см.
Из точки С как из центра чертим полуокружность радиусом 12 см.
Точку их пересечения обозначим В.
Соединим А и В. Косинус угла ВАС=АС:АВ=5/13.
Косинус смежного ∠ВАМ= -5/13. Это искомый угол.
Из точки С по общепринятому методу возводим перпендикуляр. На нем откладываем катет СВ=12 см.
Соединяем В и А. В построенном треугольнике косинус угла А равен 5/13. Смежный ему тупой угол ВАМ - искомый, его косинус - 5/13.
На листочке в клеточку отмечено три точки F, S, D. Известно , что площадь одной клеточки 4 см². Рассчитайте расстояние от F до SD в метрах.
Объяснение:
Расстояние это перпендикуляр. Пусть FH⊥SD. Тогда FH расстояние до SD.
Найдем длину квадрата площадью 4 см² ⇒2*2=4, значит сторона квадрата 2 см.
Пусть SК⊥FD . Найдем площадь ΔFSD
S=1/2*FD*SK , S=1/2*8*6=24 (см²).
С другой стороны S( ΔFSD)=1/2*SD*FH .Нахождение SD внизу.
24=1/2*6√2*FH ⇒FH=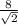
, FH=4√2 см=0,04√2 м
Расстояние от F до SD 0,04√2 м
==================
В желтом прямоугольном треугольнике , со стороной 6 см, по т. Пифагора, SD=√(6²+6²)=√(2*6²)=6√2 ( cм)