Можно решать через формулы для количества информации в сообщении, записанном алфавитом с известным количеством символов.
Здесь алфавит- это набор всех возможных значений показаний прибора (каждое из возможных показаний- один из символов алфавита). Значит, мощность алфавита равна:
символов
Было сделано 50 измерений, и соответственно записано 50 значений показаний прибора. Каждая из этих записей- это один символ, записанный в сообщении. Значит, длина сообщения равна:
символов
Далее, количество информации в одном символе ( ) можно найти двумя путями:
1) Через формулу . Просто подбираем (по таблице степеней двойки или считая на калькуляторе) такое минимальное целое значение , чтобы два в этой степени дало значение не меньше чем символов. Например:
(меньше чем 100, не хватит для всех символов нашего алфавита)
(не меньше 100, достаточно для хранения всех 100 значений)
То есть, минимальная нужная нам степень равна 7. Значит, количество информации в одном символе (для нашего алфавита) равно:
бит
2) Если вы уже проходили формулу расчёта через двоичный логарифм, то можно считать по ней. При этом, двоичный логарифм (которого может не быть в калькуляторе) можно заменить отношением десятичных либо натуральных логарифмов:
Раз получилось дробное значение, то выбираем следующее целое (большее, чем полученное по расчёту). То есть, число 7. Другими словами, округляем до целых, но не как обычно, а всегда в большую сторону. Опять же, мы получили, что:
бит
Далее, считаем количество информации в сообщении (информационный размер сообщения):
бит
Переводим в байты:
Б
Это значение тоже можно было бы округлить до целых (всегда в большую сторону), ведь при хранении чаще всего хранят целое число байт. Но, в задаче не сказано про именно целое число байт, поэтому не будем округлять.
Можно решать через формулы для количества информации в сообщении, записанном алфавитом с известным количеством символов.
Здесь алфавит- это набор всех возможных значений показаний прибора (каждое из возможных показаний- один из символов алфавита). Значит, мощность алфавита равна:
Было сделано 50 измерений, и соответственно записано 50 значений показаний прибора. Каждая из этих записей- это один символ, записанный в сообщении. Значит, длина сообщения равна:
Далее, количество информации в одном символе (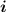
) можно найти двумя путями:
1) Через формулу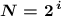
. Просто подбираем (по таблице степеней двойки или считая на калькуляторе) такое минимальное целое значение 
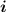, чтобы два в этой степени дало значение не меньше чем 
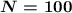символов. Например:
То есть, минимальная нужная нам степень равна 7. Значит, количество информации в одном символе (для нашего алфавита) равно:
2) Если вы уже проходили формулу расчёта через двоичный логарифм, то можно считать по ней. При этом, двоичный логарифм (которого может не быть в калькуляторе) можно заменить отношением десятичных либо натуральных логарифмов:
Раз получилось дробное значение, то выбираем следующее целое (большее, чем полученное по расчёту). То есть, число 7. Другими словами, округляем до целых, но не как обычно, а всегда в большую сторону. Опять же, мы получили, что:
Далее, считаем количество информации в сообщении (информационный размер сообщения):
Переводим в байты:
Это значение тоже можно было бы округлить до целых (всегда в большую сторону), ведь при хранении чаще всего хранят целое число байт. Но, в задаче не сказано про именно целое число байт, поэтому не будем округлять.
ответ: 43,75 байт
#include <iostream>
#include <string>
using namespace std;
int main() {
string s;
getline(cin, s);
s += ' ';
int i = 0;
while (i < (int) s.size()) {
string t;
while (s[i] != ' ') {
t += s[i];
i += 1;
}
if (t.back() != 'a' && t.back() != 'e' && t.back() != 'i' && t.back() != 'o' && t.back() != 'u') {
cout << t << ' ';
}
i += 1;
}
return 0;
}
Объяснение: