На рисунке представлены элементы интерфейса для мобильного приложения управления светом. Давайте разберемся, какие именно элементы присутствуют на этом рисунке и как они работают:
1. Заголовок: В верхней части рисунка находится заголовок приложения. Здесь может быть указано название приложения или краткое описание его функций.
2. Меню: Слева от рисунка находится меню, которое предоставляет доступ к различным функциям приложения. В данном случае, мы можем предположить, что в меню имеется функция управления освещением.
3. Кнопки управления: Под заголовком и слева от рисунка находятся кнопки управления, предназначенные для изменения настроек освещения. Обычно такие кнопки имеют символы или иконки, обозначающие определенные действия, например, включение или выключение света.
4. Регуляторы: Под кнопками управления представлены регуляторы, которые позволяют настраивать яркость или цвет освещения. Регуляторы обычно представлены ползунками или крутилками, которые можно перемещать или вращать для достижения желаемого эффекта.
5. Индикаторы: Рядом с регуляторами находятся индикаторы, которые показывают текущие настройки освещения. Например, индикатор яркости может показывать числовое значение яркости или отображать графическую шкалу.
6. Панель настроек: Справа от рисунка находится панель настроек, которая позволяет пользователю настраивать особые функции или параметры освещения. На панели могут отображаться различные опции, такие как выбор режимов работы или установка таймера.
7. Кнопка сохранения: В нижней части рисунка находится кнопка сохранения, которая позволяет сохранить настройки освещения после внесения изменений. Пользователь может нажать на эту кнопку, чтобы применить изменения и сохранить их для будущего использования.
Все эти элементы интерфейса объединяются вместе, чтобы обеспечить простоту и удобство в использовании приложения для управления светом. Пользователь может легко настроить параметры освещения с помощью кнопок, регуляторов и индикаторов, а также изменить более сложные настройки через панель настроек. Кнопка сохранения позволяет сохранить пользовательские настройки для последующего использования.
Добрый день! Благодарю за ваш вопрос по информатике. Давайте разберемся, как решить данное задание.
На изображении представлены 6 логических выражений, и наша задача состоит в том, чтобы найти другие выражения, которые будут с ними тождественно равны. Тождественное равенство означает, что значения выражений будут всегда одинаковыми, независимо от значений переменных.
Посмотрим на данное изображение:
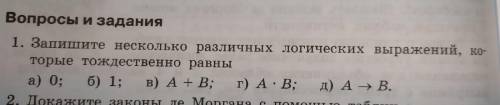
1) Разберемся с первым выражением: (A and B) or (A and not B)
Для поиска тождественно равных выражений нам нужно изменять значения переменных A и B таким образом, чтобы они были одновременно истинными или одновременно ложными.
Мы можем изменить это выражение следующим образом: (A and B) or (A and not B) = A.
Объяснение: Когда A и B имеют одно и то же значение (истина или ложь), первое выражение всегда будет равно значению A. Например, если A=истина и B=истина, то (A and B) равно истине, а (A and not B) равно лжи. Таким образом, (A and B) or (A and not B) равно истине. Если A=ложь и B=ложь, то и первое выражение равно лжи.
2) Перейдем ко второму выражению: A or (B and not A)
В данном случае мы также хотим найти другое выражение, которое будет с ним тождественно равно. Заметим, что при значении A=истина второе выражение всегда будет равно истине, независимо от значения B. Поэтому мы можем записать тождественно равное выражение: A.
3) Рассмотрим третье выражение: (A or B) and (A or not B)
Также смотрим, какое другое выражение будет с ним тождественно равным. Мы можем заметить, что когда A=ложь, весьма второе выражение равно истине, независимо от значения переменной B. Поэтому мы можем записать тождественно равное выражение: not B.
4) Проанализируем выражение: A
Также стоит отметить, что само выражение A является тождественно равным самому себе. Ведь независимо от значения переменной A, оно всегда будет равно самому себе.
5) Посмотрим на пятое выражение: not B
Точно так же как и предыдущие выражения, выражение not B равно самому себе независимо от значения переменной B.
Таким образом, мы получили несколько различных логических выражений, которые тождественно равны выражениям, представленным на изображении:
1) (A and B) or (A and not B) = A
2) A or (B and not A) = A
3) (A or B) and (A or not B) = not B
4) A
5) not B
Надеюсь, я смог достаточно подробно разъяснить решение задания по информатике. Если остались какие-либо вопросы или нужна дополнительная помощь, пожалуйста, не стесняйтесь обратиться ко мне. Я всегда готов помочь.
1. Заголовок: В верхней части рисунка находится заголовок приложения. Здесь может быть указано название приложения или краткое описание его функций.
2. Меню: Слева от рисунка находится меню, которое предоставляет доступ к различным функциям приложения. В данном случае, мы можем предположить, что в меню имеется функция управления освещением.
3. Кнопки управления: Под заголовком и слева от рисунка находятся кнопки управления, предназначенные для изменения настроек освещения. Обычно такие кнопки имеют символы или иконки, обозначающие определенные действия, например, включение или выключение света.
4. Регуляторы: Под кнопками управления представлены регуляторы, которые позволяют настраивать яркость или цвет освещения. Регуляторы обычно представлены ползунками или крутилками, которые можно перемещать или вращать для достижения желаемого эффекта.
5. Индикаторы: Рядом с регуляторами находятся индикаторы, которые показывают текущие настройки освещения. Например, индикатор яркости может показывать числовое значение яркости или отображать графическую шкалу.
6. Панель настроек: Справа от рисунка находится панель настроек, которая позволяет пользователю настраивать особые функции или параметры освещения. На панели могут отображаться различные опции, такие как выбор режимов работы или установка таймера.
7. Кнопка сохранения: В нижней части рисунка находится кнопка сохранения, которая позволяет сохранить настройки освещения после внесения изменений. Пользователь может нажать на эту кнопку, чтобы применить изменения и сохранить их для будущего использования.
Все эти элементы интерфейса объединяются вместе, чтобы обеспечить простоту и удобство в использовании приложения для управления светом. Пользователь может легко настроить параметры освещения с помощью кнопок, регуляторов и индикаторов, а также изменить более сложные настройки через панель настроек. Кнопка сохранения позволяет сохранить пользовательские настройки для последующего использования.
На изображении представлены 6 логических выражений, и наша задача состоит в том, чтобы найти другие выражения, которые будут с ними тождественно равны. Тождественное равенство означает, что значения выражений будут всегда одинаковыми, независимо от значений переменных.
Посмотрим на данное изображение:
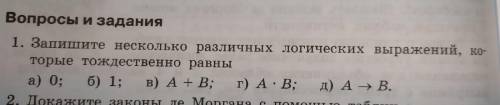
1) Разберемся с первым выражением: (A and B) or (A and not B)
Для поиска тождественно равных выражений нам нужно изменять значения переменных A и B таким образом, чтобы они были одновременно истинными или одновременно ложными.
Мы можем изменить это выражение следующим образом: (A and B) or (A and not B) = A.
Объяснение: Когда A и B имеют одно и то же значение (истина или ложь), первое выражение всегда будет равно значению A. Например, если A=истина и B=истина, то (A and B) равно истине, а (A and not B) равно лжи. Таким образом, (A and B) or (A and not B) равно истине. Если A=ложь и B=ложь, то и первое выражение равно лжи.
2) Перейдем ко второму выражению: A or (B and not A)
В данном случае мы также хотим найти другое выражение, которое будет с ним тождественно равно. Заметим, что при значении A=истина второе выражение всегда будет равно истине, независимо от значения B. Поэтому мы можем записать тождественно равное выражение: A.
3) Рассмотрим третье выражение: (A or B) and (A or not B)
Также смотрим, какое другое выражение будет с ним тождественно равным. Мы можем заметить, что когда A=ложь, весьма второе выражение равно истине, независимо от значения переменной B. Поэтому мы можем записать тождественно равное выражение: not B.
4) Проанализируем выражение: A
Также стоит отметить, что само выражение A является тождественно равным самому себе. Ведь независимо от значения переменной A, оно всегда будет равно самому себе.
5) Посмотрим на пятое выражение: not B
Точно так же как и предыдущие выражения, выражение not B равно самому себе независимо от значения переменной B.
Таким образом, мы получили несколько различных логических выражений, которые тождественно равны выражениям, представленным на изображении:
1) (A and B) or (A and not B) = A
2) A or (B and not A) = A
3) (A or B) and (A or not B) = not B
4) A
5) not B
Надеюсь, я смог достаточно подробно разъяснить решение задания по информатике. Если остались какие-либо вопросы или нужна дополнительная помощь, пожалуйста, не стесняйтесь обратиться ко мне. Я всегда готов помочь.