Задания типа 1, 2 решаются с знаний систем счисления и степеней:
а) Приводим все степени к одному основанию (равному основанию системы счисления, в которой потом нужно записать результат). Последнее слагаемое тоже нужно разложить на сумму/разность нескольких степеней (например, или ).
б) Представляем, как выглядит каждое из этих чисел в данной системе счисления (как единица с количеством нулей после неё, равным показателю степени, например ).
в) Делаем сложение, а затем- вычитание чисел (оба раза- от большего (по модулю) числа к меньшему). Не нужно полностью писать числа, нужно посчитать, сколько появится нулей/единиц между таким то и таким то разрядом, если сложить/вычесть одно из другого (тут нужно понимать, как происходит сложение/вычитание в той или иной системе счисления).
Пример №1:
В двоичной системе эти слагаемые выглядят как:
единица и 4028 нулей (то есть, ),
единица и 2015 нулей (то есть, ),
единица и 3 нуля (то есть ),
единица без нулей (то есть, ).
Складываем первые два слагаемых (представляем в уме). Получится следующее двоичное число:
1 (2012 нулей) 1 (2015 нулей) ₂
Итого, тут пока только две единицы.
Затем, вычитаем отсюда число 1000₂ Получим вот что:
1 (2012 нулей) 0 (2011 единиц) 1000₂
Итого, тут уже 2013 единиц.
Далее, вычитаем отсюда 1₂ Получаем вот что:
1 (2012 нулей) 0 (2011 единиц) 0111₂
Итого, тут получилось ровно 2015 единиц.
Пример №2:
В двоичной системе эти слагаемые выглядят как:
1) единица и 12072 нуля,
2) единица и 3210 нулей,
3) единица и 1024 нуля,
4) единица и 7 нулей (то есть ),
5) единица и 1 нуль (то есть, ).
Складываем большие положительные слагаемые (№ 1 и 3). Получим:
Если сложить это в двоичном виде, то число разрядов останется такое же, как было в большем слагаемом (оно в двоичном виде выглядело как единица и 1026 нулей, т.е. всего 1027 разрядов).
Каждые три двоичных разряда дают один восьмеричный. Разбивают число начиная от десятичной запятой. То есть, можно поделить 1026 / 3 = 342 восьмеричных разряда, и ещё один разряд (идущий в начале числа)- там уже не обязательно иметь три разряда, всё равно он даст на выходе один восьмеричный разряд. Итого 342 + 1 = 343 восьмеричных разряда.
Другими словами, можно взять общее число двоичных разрядов (1027), поделить на три и если число получилось дробное- то округлить вверх (т.е. не обычное округление, а всегда вверх, с избытком).
Задания типа 1, 2 решаются с знаний систем счисления и степеней:
а) Приводим все степени к одному основанию (равному основанию системы счисления, в которой потом нужно записать результат). Последнее слагаемое тоже нужно разложить на сумму/разность нескольких степеней (например,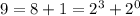 или
или 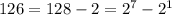 ).
).
б) Представляем, как выглядит каждое из этих чисел в данной системе счисления (как единица с количеством нулей после неё, равным показателю степени, например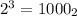 ).
).
в) Делаем сложение, а затем- вычитание чисел (оба раза- от большего (по модулю) числа к меньшему). Не нужно полностью писать числа, нужно посчитать, сколько появится нулей/единиц между таким то и таким то разрядом, если сложить/вычесть одно из другого (тут нужно понимать, как происходит сложение/вычитание в той или иной системе счисления).
Пример №1:
В двоичной системе эти слагаемые выглядят как:
единица и 4028 нулей (то есть,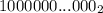 ),
),
единица и 2015 нулей (то есть, ),
),
единица и 3 нуля (то есть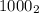 ),
),
единица без нулей (то есть,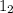 ).
).
Складываем первые два слагаемых (представляем в уме). Получится следующее двоичное число:
1 (2012 нулей) 1 (2015 нулей) ₂
Итого, тут пока только две единицы.
Затем, вычитаем отсюда число 1000₂ Получим вот что:
1 (2012 нулей) 0 (2011 единиц) 1000₂
Итого, тут уже 2013 единиц.
Далее, вычитаем отсюда 1₂ Получаем вот что:
1 (2012 нулей) 0 (2011 единиц) 0111₂
Итого, тут получилось ровно 2015 единиц.
Пример №2:
В двоичной системе эти слагаемые выглядят как:
1) единица и 12072 нуля,
2) единица и 3210 нулей,
3) единица и 1024 нуля,
4) единица и 7 нулей (то есть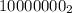 ),
),
5) единица и 1 нуль (то есть,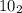 ).
).
Складываем большие положительные слагаемые (№ 1 и 3). Получим:
1 (11047 нулей) 1 (1024 нуля) ₂
Итого, тут пока только две единицы.
Затем, вычитаем отсюда слагаемое № 2 Получим:
(8862 единиц) (2185 нулей) 1 (1024 нуля) ₂
Итого, тут уже 8863 единицы.
Далее, вычитаем 10000000₂ Получаем вот что:
(8862 единиц) (2185 нулей) 0 (1016 единиц) 10000000₂
Итого, тут сейчас 9879 единиц.
Далее, вычитаем отсюда 10₂ Получаем вот что:
(8862 единиц) (2185 нулей) 0 (1016 единиц) 01111110₂
Итого, тут получилось ровно 9884 единицы.
Задание № 3:
Если сложить это в двоичном виде, то число разрядов останется такое же, как было в большем слагаемом (оно в двоичном виде выглядело как единица и 1026 нулей, т.е. всего 1027 разрядов).
Каждые три двоичных разряда дают один восьмеричный. Разбивают число начиная от десятичной запятой. То есть, можно поделить 1026 / 3 = 342 восьмеричных разряда, и ещё один разряд (идущий в начале числа)- там уже не обязательно иметь три разряда, всё равно он даст на выходе один восьмеричный разряд. Итого 342 + 1 = 343 восьмеричных разряда.
Другими словами, можно взять общее число двоичных разрядов (1027), поделить на три и если число получилось дробное- то округлить вверх (т.е. не обычное округление, а всегда вверх, с избытком).
1,035 Кбайт
Объяснение:
I = K * i
I - информационный объём текста рассказа (размер файла, содержащего рассказ)
K - количество символов в рассказе
i - информационный вес одного символа (число бит, используемых для записи одного символа)
N <= 2^i
N - мощность алфавита (количество символов в алфавите)
i - информационный вес одного символа (число бит, используемых для записи одного символа)
Дано:
K = 8 странице * 4 строки * 53 символа = 1 696 символов
N = 20 символов
Найти:
I (Кбайт)
20 <= 2^i
20 <= 2^5
i = 5 бит
I = 1 696 * 5 = 8 480 бит = 1 060 байт = 1,035 Кбайт
8 бит = 1 байт
1 024 байт = 1 Кбайт