Два игрока, петя и ваня, играют в следующую игру. перед ними лежат две кучки камней, в первой из которых 4, а во второй - 3 камня. у каждого игрока неограниченно много камней. игроки ходят по очереди, первый ход делает петя. ход состоит в том, что игрок или утраивает число камней в какой-то куче, или добавляет 1 камень в какую-то кучу. игра завершается в тот момент, когда общее количество камней в двух кучах становится не менее 20. если в момент завершения игры общее число камней в двух кучах не менее 35, то выиграл ваня, в противном случае - петя. кто выигрывает при безошибочной игре обоих игроков? укажите, стратегию выигрывающего игрока - какой ход он должен сделать в каждой из позиций, которые могут ему встретиться при правильной игре. докажите, что описанная стратегия - выигрышная.

Это таблица истинности для логических функций. Галочка вверх означает логическое И, галочка вниз - логическое ИЛИ, уголок перед переменной - логическое НЕ. Это тема обширная, и так что если я представлю здесь решение это все равно вам не понять. Вам нужно почитать о логических функциях и таблицах истинности.

Вот как выглядит решение. Поставляем значения из таблицы истинности в варианты функций. Та функция, результат которой совпадает с результатом из таблицы, является ответом. В данном случае это номер 2

2018 2020 1931 2109

Объяснение:

Последние элементы n-й строки образуют последовательность a(n)=n^2.

44<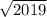<45 ⇒ число 2019 расположено в 45=й строке.

Первые элементы n-й строки образуют последовательность b(n)=(n-1)^2+1.

(45-1)^2+1=1937 ⇒ 2019 не является первым элементом строки.

Поскольку число 2019 не является ни первым, ни последним элементом строки, у числа 2019 существует соседнее слева (2018) и  соседнее справа (2020) число.

Для любого элемента n-й строки справедливо равенство c(n)-c(n-1)=(n-1)*2

Вычисляем верхнее соседнее число.

(45-1)*2=88

2019-88=1931

Вычисляем нижнее соседнее число.

(46-1)*2=90

2019+90=2109