На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1) Строится двоичная запись числа N. 2) К этой записи дописываются справа ещё два разряда по следующему правилу: a) складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001; b) над этой записью производятся те же действия – справа дописывается остаток от деления суммы цифр на 2. Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите такое наименьшее число N, для которого результат работы алгоритма больше 45. В ответе это число запишите в десятичной системе счисления.
11
Объяснение:
Если изначально сумма разрядов была чётная, то в конец запишется 00, что эквивалентно .
.
Если же сумма была нечётная, то запишется 10, что эквивалентно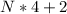 .
.
В обоих случаях число получается чётным.
Посмотрим на чётные числа, превосходящие 45.
============
Не забывайте нажать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"
Бодрого настроения и добра!
Успехов в учебе