На вход алгоритма подаётся натуральное число n. алгоритм строит по нему новое число r следующим образом. 1) строится двоичная запись числа n. 2) к этой записи дописываются справа ещё два разряда по следующему правилу: а) складываются все цифры двоичной записи числа n, и остаток от деления суммы на 2 дописывается в конец числа (справа). например, запись 101010 преобразуется в запись 1010101; б) над этой записью производятся те же действия – справа дописывается остаток от деления суммы её цифр на 2. полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа n) является двоичной записью искомого числа r. укажите минимальное число r, которое превышает число 126 и может являться результатом работы данного алгоритма. в ответе это число запишите в десятичной системе счисления.
130
Объяснение:
Заметим, что большему результату соответствует большее исходное число. Значит, можно найти минимально возможное исходное число, проделать над ним все необходимые действия, и получить R.
Поскольку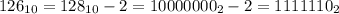 , исходное число не может быть меньше
, исходное число не может быть меньше 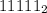 . Проверяем:
. Проверяем: 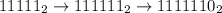 - это не больше 126, не подходит.
- это не больше 126, не подходит.
Следующий кандидат для исходного числа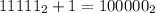 .
.
Осталось перевести R в десятичную систему счисления