Написать программу для решения (все в одной программе). показать диалог с пользователем (вывод сообщений и полученных значений). решить в кумире введено трехзначное число x а) вывести цифры этого числа (а, b, с) б) проверить, образуют ли цифры этого числа палиндром? в) образуют ли цифры данного числа возрастающую последовательность? г) определить и вывести максимальную цифру данного числа д) определить сумму чисел полученного числа (s) е) определить, является ли число s четным и кратным 3 ж) определить принадлежит ли число s интервалу (10 з) вывести перевертыш этого числа (справа налево)

#include <iostream>

int main() {

const int SIZE = 10;

bool isSence = false;

int sum = 0;

int count = 0;

int arr[SIZE];

for (int i = 0; i < SIZE; i++)

{

 arr[i] = rand() % 20 - 10; // "рандомно" заполняем массив от -10 до 10

 std::cout << arr[i] << "\t"; // выводим массив в консоль

 if (arr[i] >= 0)

  isSence = true;

}

for (int i = 0; i < SIZE; i++)

{

 if ((isSence) && (arr[i] > 0))

  sum += arr[i]; //sum = sum + arr[i];

  count++;

}

if (isSence)

 std::cout << "\nсреднее арифметическое положительных чисел = " << double(sum) / count << std::endl; // явное приведение типов

else

 std::cout << "\nВ массиве нету положительных чисел или нету нулей и/или отрицательных чисел" << std::endl;

return 0;

}

должно быть минимум 7 элементов

Объяснение:

Каждый излучающий элемент имеет два состояния- красный или синий цвет (выключенное состояние не рассматривается по условиям).

Значит, число возможных вариантов, которые можно показать на таком табло равно двум в степени, равной числу элементов.

Например:

один элемент: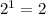  различных сигнала (состояния панели)

три элемента: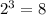  различных сигналов можно отобразить

шесть элементов: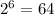  различных сигнала (мало, надо сто)

семь элементов: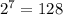  различных сигналов (нам хватит)

Выбираем семь элементов, т.к. ими можно отобразить сто вариантов (и даже немного больше).

Можно и посчитать число элементов напрямую, без подбора.

Считается через логарифм по основанию два из десяти, затем округляется с избытком (то есть, всегда вверх):

В расчёте также показано, что такой логарифм можно посчитать через отношение двух десятичных логарифмов (lg), либо двух натуральных логарифмов (ln).