(см. объяснение)
Объяснение:
Число 21 в развернутой форме записи можно представить так:
Из условия задачи следует, что последнее число в системе счисления с основанием n равно 0, т.е. .
Тогда получим:
Заметим, что n можно вынести за скобки:
Разделим обе части равенства на n:
Получили, что 21 делится на основание системы счисления без остатка.
Учитывая, что n>1, наименьший делитель числа 21 - это 3.
Поэтому минимальное основание системы счисления, при записи числа 21 в которой последним символом будет 0 равно 3.
И действительно .
Задача решена!
(см. объяснение)
Объяснение:
Число 21 в развернутой форме записи можно представить так:
Из условия задачи следует, что последнее число в системе счисления с основанием n равно 0, т.е.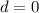 .
.
Тогда получим:
Заметим, что n можно вынести за скобки:
Разделим обе части равенства на n:
Получили, что 21 делится на основание системы счисления без остатка.
Учитывая, что n>1, наименьший делитель числа 21 - это 3.
Поэтому минимальное основание системы счисления, при записи числа 21 в которой последним символом будет 0 равно 3.
И действительно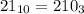 .
.
Задача решена!