Добрый день! Благодарю за ваш вопрос по информатике. Давайте разберемся, как решить данное задание.
На изображении представлены 6 логических выражений, и наша задача состоит в том, чтобы найти другие выражения, которые будут с ними тождественно равны. Тождественное равенство означает, что значения выражений будут всегда одинаковыми, независимо от значений переменных.
Посмотрим на данное изображение:
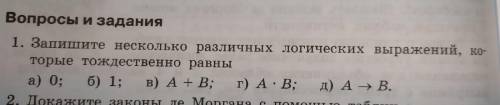
1) Разберемся с первым выражением: (A and B) or (A and not B)
Для поиска тождественно равных выражений нам нужно изменять значения переменных A и B таким образом, чтобы они были одновременно истинными или одновременно ложными.
Мы можем изменить это выражение следующим образом: (A and B) or (A and not B) = A.
Объяснение: Когда A и B имеют одно и то же значение (истина или ложь), первое выражение всегда будет равно значению A. Например, если A=истина и B=истина, то (A and B) равно истине, а (A and not B) равно лжи. Таким образом, (A and B) or (A and not B) равно истине. Если A=ложь и B=ложь, то и первое выражение равно лжи.
2) Перейдем ко второму выражению: A or (B and not A)
В данном случае мы также хотим найти другое выражение, которое будет с ним тождественно равно. Заметим, что при значении A=истина второе выражение всегда будет равно истине, независимо от значения B. Поэтому мы можем записать тождественно равное выражение: A.
3) Рассмотрим третье выражение: (A or B) and (A or not B)
Также смотрим, какое другое выражение будет с ним тождественно равным. Мы можем заметить, что когда A=ложь, весьма второе выражение равно истине, независимо от значения переменной B. Поэтому мы можем записать тождественно равное выражение: not B.
4) Проанализируем выражение: A
Также стоит отметить, что само выражение A является тождественно равным самому себе. Ведь независимо от значения переменной A, оно всегда будет равно самому себе.
5) Посмотрим на пятое выражение: not B
Точно так же как и предыдущие выражения, выражение not B равно самому себе независимо от значения переменной B.
Таким образом, мы получили несколько различных логических выражений, которые тождественно равны выражениям, представленным на изображении:
1) (A and B) or (A and not B) = A
2) A or (B and not A) = A
3) (A or B) and (A or not B) = not B
4) A
5) not B
Надеюсь, я смог достаточно подробно разъяснить решение задания по информатике. Если остались какие-либо вопросы или нужна дополнительная помощь, пожалуйста, не стесняйтесь обратиться ко мне. Я всегда готов помочь.
На изображении представлены 6 логических выражений, и наша задача состоит в том, чтобы найти другие выражения, которые будут с ними тождественно равны. Тождественное равенство означает, что значения выражений будут всегда одинаковыми, независимо от значений переменных.
Посмотрим на данное изображение:
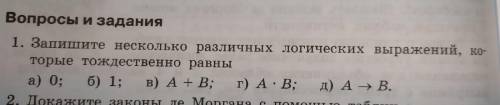
1) Разберемся с первым выражением: (A and B) or (A and not B)
Для поиска тождественно равных выражений нам нужно изменять значения переменных A и B таким образом, чтобы они были одновременно истинными или одновременно ложными.
Мы можем изменить это выражение следующим образом: (A and B) or (A and not B) = A.
Объяснение: Когда A и B имеют одно и то же значение (истина или ложь), первое выражение всегда будет равно значению A. Например, если A=истина и B=истина, то (A and B) равно истине, а (A and not B) равно лжи. Таким образом, (A and B) or (A and not B) равно истине. Если A=ложь и B=ложь, то и первое выражение равно лжи.
2) Перейдем ко второму выражению: A or (B and not A)
В данном случае мы также хотим найти другое выражение, которое будет с ним тождественно равно. Заметим, что при значении A=истина второе выражение всегда будет равно истине, независимо от значения B. Поэтому мы можем записать тождественно равное выражение: A.
3) Рассмотрим третье выражение: (A or B) and (A or not B)
Также смотрим, какое другое выражение будет с ним тождественно равным. Мы можем заметить, что когда A=ложь, весьма второе выражение равно истине, независимо от значения переменной B. Поэтому мы можем записать тождественно равное выражение: not B.
4) Проанализируем выражение: A
Также стоит отметить, что само выражение A является тождественно равным самому себе. Ведь независимо от значения переменной A, оно всегда будет равно самому себе.
5) Посмотрим на пятое выражение: not B
Точно так же как и предыдущие выражения, выражение not B равно самому себе независимо от значения переменной B.
Таким образом, мы получили несколько различных логических выражений, которые тождественно равны выражениям, представленным на изображении:
1) (A and B) or (A and not B) = A
2) A or (B and not A) = A
3) (A or B) and (A or not B) = not B
4) A
5) not B
Надеюсь, я смог достаточно подробно разъяснить решение задания по информатике. Если остались какие-либо вопросы или нужна дополнительная помощь, пожалуйста, не стесняйтесь обратиться ко мне. Я всегда готов помочь.