end_num = 79 for n in 1..5 for i in 0..2**n-1 s = ("000000000000000000000000000000" + i.to_s(2))[-n..-1] start_num = 7 log = start_num.to_s for k in 0..s.size-1
start_num, log = f0(start_num, log) if s[k] == "0" start_num, log = f1(start_num, log) if s[k] == "1" # break if start_num > end_num end # p [start_num, log, s, n] if start_num == end_num then log += " = " + end_num.to_s p log end end end
58 - не квадрат, поэтому последняя операция могла быть только вычитание 2. Значит, до этого было 60.
60 - не квадрат, поэтому следующая операция могла быть только вычитание 2. Значит, до этого было 62.
62 - не квадрат, поэтому следующая операция могла быть только вычитание 2. Значит, до этого было 64.
64 - квадрат. Учитывая, что нам нужно получить 10, если бы тут тоже было вычитание 2, то и на следующем шаге была бы такая же операция, и к пятому шагу у нас было бы 68, а не 10. Поэтому тут было возведение в квадрат, до этого было 8
8 - не квадрат, поэтому следующая операция могла быть только вычитание 2. Значит, до этого было 10 (ура!).
Теперь в обычном порядке:
Меняем все операции "-2" на 2, а "" на 1 и получаем 21222
#Ruby22
def f0(number, log)
return [number * number, "(" + log + ")^2 "]
end
def f1(number, log)
return [number - 2, log + " - 2"]
end
end_num = 79
for n in 1..5
for i in 0..2**n-1
s = ("000000000000000000000000000000" + i.to_s(2))[-n..-1]
start_num = 7
log = start_num.to_s
for k in 0..s.size-1
start_num, log = f0(start_num, log) if s[k] == "0"
start_num, log = f1(start_num, log) if s[k] == "1"
# break if start_num > end_num
end
# p [start_num, log, s, n]
if start_num == end_num then
log += " = " + end_num.to_s
p log
end
end
end
21222
Объяснение:
Как обычно, идём с конца.
58 - не квадрат, поэтому последняя операция могла быть только вычитание 2. Значит, до этого было 60.
60 - не квадрат, поэтому следующая операция могла быть только вычитание 2. Значит, до этого было 62.
62 - не квадрат, поэтому следующая операция могла быть только вычитание 2. Значит, до этого было 64.
64 - квадрат. Учитывая, что нам нужно получить 10, если бы тут тоже было вычитание 2, то и на следующем шаге была бы такая же операция, и к пятому шагу у нас было бы 68, а не 10. Поэтому тут было возведение в квадрат, до этого было 8
8 - не квадрат, поэтому следующая операция могла быть только вычитание 2. Значит, до этого было 10 (ура!).
Теперь в обычном порядке:
Меняем все операции "-2" на 2, а "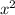 " на 1 и получаем 21222
" на 1 и получаем 21222