Первое логическое выражение(A∧B) это конъюнкция(И), которая выполняется, только когда оба условия истинны. Только первое утверждение имеет такую конструкцию(И).
Второе логическое выражение(A∨B) это дизъюнкция(ИЛИ), которая выполняется, когда хотя бы одно из условий истинно. Это второе утверждение.
Третье отличается от второго тем, что имеет знак "¬" (НЕ), который отрицает утверждение, что студент едет в метро (отрицает А). Третьему утверждению соответствует логическое выражение B∨¬A.
Из 25 сделать 31 можно только одним раз прибавив 1: любая операция "сделай нечетное" выдаст число, не меньшее . Тогда количество всех команд, которые получают 31, проходя через 25, равно количеству команд, которые просто получают 25.
Используя написанное выше, можно поступить так: посчитать количество программ, получающих 31, и вычесть из неё количество команд, получающих 25. Это и будет ответом.
Пусть a(n) - количество программ, получающих из 1 число n. Например, a(1) = a(2) = 1: 1 получает единственная (пустая) программа, а 2 можно получить при команды "прибавить 1"
Если n четное, то последняя команда в программе - прибавление 1, a(n) = a(n - 1).
Если n нечетное, то последняя команда в программе - либо прибавление 1, либо "сделай нечетное" из числа (n - 1)/2; a(n) = a(n - 1) + a((n - 1)/2).
Объяснение:
Первое логическое выражение(A∧B) это конъюнкция(И), которая выполняется, только когда оба условия истинны. Только первое утверждение имеет такую конструкцию(И).
Второе логическое выражение(A∨B) это дизъюнкция(ИЛИ), которая выполняется, когда хотя бы одно из условий истинно. Это второе утверждение.
Третье отличается от второго тем, что имеет знак "¬" (НЕ), который отрицает утверждение, что студент едет в метро (отрицает А). Третьему утверждению соответствует логическое выражение B∨¬A.
44
Объяснение:
Из 25 сделать 31 можно только одним раз прибавив 1: любая операция "сделай нечетное" выдаст число, не меньшее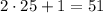 . Тогда количество всех команд, которые получают 31, проходя через 25, равно количеству команд, которые просто получают 25.
. Тогда количество всех команд, которые получают 31, проходя через 25, равно количеству команд, которые просто получают 25.
Используя написанное выше, можно поступить так: посчитать количество программ, получающих 31, и вычесть из неё количество команд, получающих 25. Это и будет ответом.
Пусть a(n) - количество программ, получающих из 1 число n. Например, a(1) = a(2) = 1: 1 получает единственная (пустая) программа, а 2 можно получить при команды "прибавить 1"
Если n четное, то последняя команда в программе - прибавление 1, a(n) = a(n - 1).
Если n нечетное, то последняя команда в программе - либо прибавление 1, либо "сделай нечетное" из числа (n - 1)/2; a(n) = a(n - 1) + a((n - 1)/2).
Начинаю считать:
a(3) = a(2) + a(1) = 2
a(4) = a(3) = 2
a(5) = a(4) + a(2) = 3
a(6) = a(5) = 3
a(7) = a(6) + a(3) = 3 + 2 = 5
... и т.д.
Итоговая таблица для всех n от 1 до 31:
ответ - это a(31) - a(25).