Алгоритм: положим в ячейку, где стоит шашка, значение 1. В некоторую ячейку с горизонталью i и вертикалью j можно добраться из клеток (i-1, j-1) и (i-1, j+1), если эти клетки существуют. Тогда для двумерного массива A, выступающего в роли доски, будет справедливо следующее утверждение: A[i+1][j] = A[i][j-1] + A[i][j+1]. Существовать ячейки не будут, если находятся в крайних столбцах: A[i+1][0] = A[i][1] и A[i+1][7] = A[i][6].
a – число десятков тысяч (первая цифра): n // 10000
b – число тысяч (вторая цифра): n % 10000 // 1000
c – число сотен (третья цифра): n % 1000 // 100
d – число десятков (четвертая цифра): n % 100 // 10
e – число единиц (пятая цифра): n % 10
Объяснение:
n %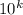
- оставляет k знаков.
n //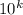
- оставляет все начиная с k+1 знака
n % 10 - остаток от деления на 10. Например: 12345 % 10 = 5
n % 100 // 10 - результат целочисленного деления на 10 остатка от деления на 100. Например: 12345 % 100 = 45; 45 // 10 = 4
n % 1000 // 100 - результат целочисленного деления на 100 остатка от деления на 1000. Например: 12345 % 1000 = 345; 345// 100 = 3
============
Не забывайте нажать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"
Бодрого настроения и добра!
Успехов в учебе!
Алгоритм: положим в ячейку, где стоит шашка, значение 1. В некоторую ячейку с горизонталью i и вертикалью j можно добраться из клеток (i-1, j-1) и (i-1, j+1), если эти клетки существуют. Тогда для двумерного массива A, выступающего в роли доски, будет справедливо следующее утверждение: A[i+1][j] = A[i][j-1] + A[i][j+1]. Существовать ячейки не будут, если находятся в крайних столбцах: A[i+1][0] = A[i][1] и A[i+1][7] = A[i][6].
Программа:
y, x = map(int, input().split())
x, y = x - 1, y - 1
board = [[0]*8 for i in range(8)]
board[x][y] = 1
for i in range(x, 7):
board[i+1][0] += board[i][1]
for j in range(1, 7):
board[i+1][j] += board[i][j-1] + board[i][j+1]
board[i+1][7] += board[i][6]
print(sum(board[7]))