В дощечку в один ряд вбиты гвоздики. Любые два гвоздика можно соединить ниточкой. Требуется соединить некоторые пары гвоздиков ниточками так, чтобы к каждому гвоздику была привязана хотя бы одна ниточка, а суммарная длина всех ниточек была минимальна.

Входные данные

В первой строке входных данных записано число N — количество гвоздиков (2≤N≤100). В следующей строке заданы N чисел — координаты всех гвоздиков (неотрицательные целые числа, не превосходящие 10000).

Выходные данные

Выведите единственное число — минимальную суммарную длину всех ниточек.

Примеры

Ввод
6
3 4 6 12 13 14

Вывод
5

=$B$3 + 5*F2

Объяснение:

Ссылки в электронной таблице:

1) Относительные ссылки - ссылки, в которых просто указываются буква столбца и номер строки (А1). При копировании изменяются: влево и в право изменяются названия столбца, вверх и вниз номер строки.

2) Абсолютные ссылки - ссылки в которых перед буквой столбца и номером строки ставится знак $ (знак неизменности ссылки) ($A$1). При копировании не изменяются.

3) Смешанные ссылки - ссылки, которые имеют признаки относительных и абсолютных ссылок одновременно ($A1 или A$1). При копировании изменяются только те столбцы или строки перед которыми нет знака $.

=$B$3 + 5*E1 - формула в ячейке C4 содержит 2 вида ссылок

Левая часть $B$3 представляет собой абсолютную ссылку, которая при копировании не изменится

После копирования левая часть останется без изменений: $B$3

Правая часть 5*E1 содержит относительную ссылку (E1), которая изменится при копировании.

Ячейка в которую копируется формула (D5), находится на 1 столбец правее и на 1 строку ниже, чем исходная ячейка (C4).

Следовательно и столбец и строка копируемой относительной ссылки изменится на 1. Столбец E будет заменён следующим за ним столбцом F, а строка будет увеличена на 1, т.е. станет равна 2 (1 + 1 = 2).

После копирования правая часть примет вид: 5*F2

44

Объяснение:

Из 25 сделать 31 можно только одним раз прибавив 1: любая операция "сделай нечетное" выдаст число, не меньшее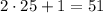 . Тогда количество всех команд, которые получают 31, проходя через 25, равно количеству команд, которые просто получают 25.

Используя написанное выше, можно поступить так: посчитать количество программ, получающих 31, и вычесть из неё количество команд, получающих 25. Это и будет ответом.

Пусть a(n) - количество программ, получающих из 1 число n. Например, a(1) = a(2) = 1: 1 получает единственная (пустая) программа, а 2 можно получить при команды "прибавить 1"

Если n четное, то последняя команда в программе - прибавление 1, a(n) = a(n - 1).

Если n нечетное, то последняя команда в программе - либо прибавление 1, либо "сделай нечетное" из числа (n - 1)/2; a(n) = a(n - 1) + a((n - 1)/2).

Начинаю считать:

a(3) = a(2) + a(1) = 2

a(4) = a(3) = 2

a(5) = a(4) + a(2) = 3

a(6) = a(5) = 3

a(7) = a(6) + a(3) = 3 + 2 = 5

... и т.д.

Итоговая таблица для всех n от 1 до 31:

ответ - это a(31) - a(25).