nh = A div C - количество квадратов умещающихся по-вертикали
nw = B div C - количество квадратов умещающихся по-горизонтали
n = nh * nw = общее количество квадратов.
Sr = A * B - 2*C*C
Код:
using System;namespace ThisAnswerIsNotMine { class Program { private static void Eq(double a) { var x = Math.Atan(1 / (Math.Exp(a) + 1)) + Math.PI; Console.WriteLine($"Для a = {a}, x = {x}"); } private static void Squares(int A, int B, int C) { int nh = A / C; int nw = B / C; int n = nh * nw; int Sr = A * B - 2*C*C; Console.WriteLine($"Количество квадратов со стороной {C} в прямоугольнике размером {A}x{B} равно: {n}"); Console.WriteLine($"Площадь оставшегося куска {Sr}"); } private static void Main() { Eq(double.Parse(Console.ReadLine()!)); Squares(int.Parse(Console.ReadLine()!), int.Parse(Console.ReadLine()!), int.Parse(Console.ReadLine()!)); } }}
1) ( (x ∈ P) /\ (x ∈ А)) → ( (x ∈ Q) /\ (x ∈ А)) = 1 -( (x ∈ P) /\ (x ∈ А)) \/ ( (x ∈ Q) /\ (x ∈ А)) = 1 (убрали стрелочку) -(x ∈ P) \/ -(x ∈ А) \/ ((x ∈ Q) /\ (x ∈ А)) = 1 (правило де Моргана) -(x ∈ P) \/ (-(x ∈ А) \/ (x ∈ Q)) /\ (-(x ∈ А) \/ (x ∈ А)) = 1 -(x ∈ P) \/ -(x ∈ А) \/ (x ∈ Q) = 1 x ∈ (-P U Q U -A) = 1 т.е. -P U Q U -A = (-infinity; +infinity) -P U Q = (-infinity; 39) U (58; +infinity) нужно чтоб -А покрыло оставшийся кусок [39; 58] т.е. А не должно содержать [39; 58] из предложенных это 1) [5, 20]
2) Алфавит из 18 символов, log(18)/log(2) = 4.16992500144231 {округляем до целого} ~= 5 бит на символ Вес номера байт = 5бит * 6 / 8 = 3.75 байт {округляем до целого} ~= 4 байт 400 * 4 байт = 1600 байт
3) Комбинаторика - Размещение с повторениями n - кол-во элементов в наборе (у нас 4) k - кол-во мест (у нас 5 и 6) Количество размещений с повторениями = `A(k,n) = n^k `A(5, 4) + `A(6, 4) = 4^5 + 4^6 = 5 120
Для получения корня между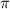
и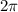 
n = 1.
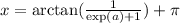
Задние 2nh = A div C - количество квадратов умещающихся по-вертикали
nw = B div C - количество квадратов умещающихся по-горизонтали
n = nh * nw = общее количество квадратов.
Sr = A * B - 2*C*C
Код:
using System;namespace ThisAnswerIsNotMine { class Program { private static void Eq(double a) { var x = Math.Atan(1 / (Math.Exp(a) + 1)) + Math.PI; Console.WriteLine($"Для a = {a}, x = {x}"); } private static void Squares(int A, int B, int C) { int nh = A / C; int nw = B / C; int n = nh * nw; int Sr = A * B - 2*C*C; Console.WriteLine($"Количество квадратов со стороной {C} в прямоугольнике размером {A}x{B} равно: {n}"); Console.WriteLine($"Площадь оставшегося куска {Sr}"); } private static void Main() { Eq(double.Parse(Console.ReadLine()!)); Squares(int.Parse(Console.ReadLine()!), int.Parse(Console.ReadLine()!), int.Parse(Console.ReadLine()!)); } }}( (x ∈ P) /\ (x ∈ А)) → ( (x ∈ Q) /\ (x ∈ А)) = 1
-( (x ∈ P) /\ (x ∈ А)) \/ ( (x ∈ Q) /\ (x ∈ А)) = 1 (убрали стрелочку)
-(x ∈ P) \/ -(x ∈ А) \/ ((x ∈ Q) /\ (x ∈ А)) = 1 (правило де Моргана)
-(x ∈ P) \/ (-(x ∈ А) \/ (x ∈ Q)) /\ (-(x ∈ А) \/ (x ∈ А)) = 1
-(x ∈ P) \/ -(x ∈ А) \/ (x ∈ Q) = 1
x ∈ (-P U Q U -A) = 1
т.е. -P U Q U -A = (-infinity; +infinity)
-P U Q = (-infinity; 39) U (58; +infinity)
нужно чтоб -А покрыло оставшийся кусок [39; 58] т.е. А не должно содержать [39; 58]
из предложенных это 1) [5, 20]
2) Алфавит из 18 символов, log(18)/log(2) = 4.16992500144231 {округляем до целого} ~= 5 бит на символ
Вес номера байт = 5бит * 6 / 8 = 3.75 байт {округляем до целого} ~= 4 байт
400 * 4 байт = 1600 байт
3) Комбинаторика - Размещение с повторениями
n - кол-во элементов в наборе (у нас 4)
k - кол-во мест (у нас 5 и 6)
Количество размещений с повторениями = `A(k,n) = n^k
`A(5, 4) + `A(6, 4) = 4^5 + 4^6 = 5 120