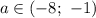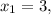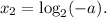Пошаговое объяснение:
(13-9,5:3,8)×0,3=3,15
1) 2)
9,5 |_3, 8__ 1 3, 0
9 5 |_3 8__ - 2, 5
- 7 6 | 2, 5 ————
—— 1 0, 5
1 9 0
- 1 9 0
———
0
3)
1 0, 5
× 0, 3
————-
3, 1 5
1) 9,5:3,8=2,5
2) 13-2,5=10,5
3) 10,5×0,3=3,15
(16,1:4,6-3,07)×0,2=0,086
1 6, 1 |_4, 6__ 3, 5 0
1 6 1 |_4 6__ - 3, 0 7
- 1 3 8 | 3, 5 —————
——— 0, 4 3
2 3 0
- 2 3 0
————
0, 4 3
× 0, 2
0, 0 8 6
1) 16,1:4,6=3,5
2) 3,5-3,07=0,43
3) 0,43×0,2=0,086
(1,3×2,8+1):0,8=5,8
1, 3 3, 6 4
× 2, 8 + 1, 0 0
———- —————
1 0 4 4, 6 4
+ 2 6
3,6 4
4, 6 4|_0, 8__
4 6,4|_8___
- 4 0 | 5, 8
——-
6 4
- 6 4
1) 1,3×2,8=3,64
2) 3,64+1=4,64
3) 4,64:0,8=5,8
(3,7×2,3-5):0,3=11,7
3, 7 8, 5 1
×2, 3 - 5, 00
——— ————
1 1 1 3, 51
+ 7 4
8, 5 1
3, 5 1|_0, 3__
3 5,1 |_3___
- 3 | 1 1, 7
——
5
- 3
2 1
- 2 1
1) 3,7×2,3=8,51
2) 8,51-5=3,51
3) 3,51:0,3=11,7
при
1)
2) Данное уравнение равносильно такой совокупности:
Первое уравнение было решено выше.
Рассмотрим систему
Уравнение системы — полный квадрат Поэтому
Так как функция принимает только положительные значения при всех при данное уравнение корней не имеет, а при
Решим неравенство системы:
Так как функция является возрастающей и учитывая ее область определения, получаем
Таким образом число будет являться корнем исходного уравнения только тогда, когда будет удовлетворять неравенству
Так как функция является возрастающей,
Выяснили, что данное уравнение всегда будет иметь корень а корень — только при
Отдельно можно выделить случай, когда оба эти корня совпадают:
Итак,
Пошаговое объяснение:
(13-9,5:3,8)×0,3=3,15
1) 2)
9,5 |_3, 8__ 1 3, 0
9 5 |_3 8__ - 2, 5
- 7 6 | 2, 5 ————
—— 1 0, 5
1 9 0
- 1 9 0
———
0
3)
1 0, 5
× 0, 3
————-
3, 1 5
1) 9,5:3,8=2,5
2) 13-2,5=10,5
3) 10,5×0,3=3,15
(16,1:4,6-3,07)×0,2=0,086
1) 2)
1 6, 1 |_4, 6__ 3, 5 0
1 6 1 |_4 6__ - 3, 0 7
- 1 3 8 | 3, 5 —————
——— 0, 4 3
2 3 0
- 2 3 0
————
0
3)
0, 4 3
× 0, 2
————
0, 0 8 6
1) 16,1:4,6=3,5
2) 3,5-3,07=0,43
3) 0,43×0,2=0,086
(1,3×2,8+1):0,8=5,8
1) 2)
1, 3 3, 6 4
× 2, 8 + 1, 0 0
———- —————
1 0 4 4, 6 4
+ 2 6
————
3,6 4
3)
4, 6 4|_0, 8__
4 6,4|_8___
- 4 0 | 5, 8
——-
6 4
- 6 4
———
0
1) 1,3×2,8=3,64
2) 3,64+1=4,64
3) 4,64:0,8=5,8
(3,7×2,3-5):0,3=11,7
1) 2)
3, 7 8, 5 1
×2, 3 - 5, 00
——— ————
1 1 1 3, 51
+ 7 4
————
8, 5 1
3)
3, 5 1|_0, 3__
3 5,1 |_3___
- 3 | 1 1, 7
——
5
- 3
——
2 1
- 2 1
——
0
1) 3,7×2,3=8,51
2) 8,51-5=3,51
3) 3,51:0,3=11,7
при![a \in ( - \infty ;\,\, - 8] \cup [ - 1;\,\, + \infty )\ x = 3;](/tpl/images/4978/6766/bd071.png)
при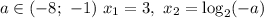
Пошаговое объяснение:
1)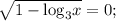
2) Данное уравнение равносильно такой совокупности:
Первое уравнение было решено выше.
Рассмотрим систему
Уравнение системы — полный квадрат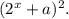 Поэтому
Поэтому
Так как функция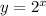 принимает только положительные значения при всех
принимает только положительные значения при всех 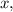 при
при 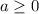 данное уравнение корней не имеет, а при
данное уравнение корней не имеет, а при 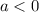
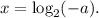
Решим неравенство системы:
Так как функция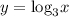 является возрастающей и учитывая ее область определения, получаем
является возрастающей и учитывая ее область определения, получаем 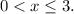
Таким образом число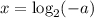 будет являться корнем исходного уравнения только тогда, когда будет удовлетворять неравенству
будет являться корнем исходного уравнения только тогда, когда будет удовлетворять неравенству 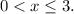
Так как функция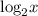 является возрастающей,
является возрастающей,
Выяснили, что данное уравнение всегда будет иметь корень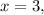 а корень
а корень 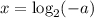 — только при
— только при 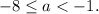
Отдельно можно выделить случай, когда оба эти корня совпадают:
Итак,
при![a \in ( - \infty ;\,\, - 8] \cup [ - 1;\,\, + \infty )](/tpl/images/4978/6766/43746.png)
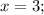
при