Обозначим за x количество окрыток у Асем, за y - у Сауле.
У Асем было в 4 раза больше:
После того, как Асем отдала 52 открытки подружке, у нее стало в 2 раза больше, чем у Сауле:
.
Подставим 4у вместо х, и решим ур-ние относительно у:
.
Чтобы избавиться от знаменателя, умножим обе части ур-я на y+52:
Перенесем свободные члены и неизвестные в разные части ур-я
- мы нашли, сколько открыток было вначале у Сауле
тогда у Асем было в 4 раза больше: .
Теперь проверим решения, подсчитав количество открыток после того, как Асем поделилась открытками с подружкой. Она отдала 52 открытки, а Сауле получила 52 открытки
,
Как и сказано в условии, у Асем стало в два раза больше открыток, чем у Сауле.
Число {\displaystyle \pi }\pi иррационально, то есть его значение не может быть точно выражено в виде дроби {\displaystyle {\frac {m}{n}}}{\frac {m}{n}}, где {\displaystyle m}m — целое число, а {\displaystyle n}n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. Иррациональность числа {\displaystyle \pi }\pi была впервые доказана Иоганном Ламбертом в 1761 году[2] путём разложения тангенса в непрерывную дробь. В 1794 году Лежандр привёл более строгое доказательство иррациональности чисел {\displaystyle \pi }\pi и {\displaystyle \pi ^{2}}\pi ^{2}. Несколько доказательств подробно приведено в статье Доказательства иррациональности π.
{\displaystyle \pi }\pi — трансцендентное число, то есть оно не может быть корнем какого-либо многочлена с целыми коэффициентами. Трансцендентность числа {\displaystyle \pi }\pi была доказана в 1882 году профессором Кёнигсбергского, а позже Мюнхенского университета Линдеманом. Доказательство упростил Феликс Клейн в 1894 году[3]. Поскольку в евклидовой геометрии площадь круга и длина окружности являются функциями числа {\displaystyle \pi }\pi , то доказательство трансцендентности {\displaystyle \pi }\pi положило конец попыткам построить квадратуру круга, длившимся более 2,5 тысяч лет.
В 1934 году Гельфонд доказал[4] трансцендентность числа {\displaystyle e^{\pi }}e^{\pi }. В 1996 году Юрий Нестеренко доказал, что для любого натурального {\displaystyle n}n числа {\displaystyle \pi }\pi и {\displaystyle e^{\pi {\sqrt {ne^{\pi {\sqrt {n}}} алгебраически независимы, откуда, в частности, следует[5][6] трансцендентность чисел {\displaystyle \pi +e^{\pi },\pi e^{\pi }}\pi +e^{\pi },\pi e^{\pi } и {\displaystyle e^{\pi {\sqrt {ne^{\pi {\sqrt {n}}}.
{\displaystyle \pi }\pi является элементом кольца периодов (а значит, вычислимым и арифметическим числом). Но неизвестно, принадлежит ли {\displaystyle 1/\pi }1/\pi к кольцу периодов.
У Асем было 312 открыток, у Сауле - 78 открыток
Пошаговое объяснение:
Обозначим за x количество окрыток у Асем, за y - у Сауле.
У Асем было в 4 раза больше: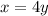
После того, как Асем отдала 52 открытки подружке, у нее стало в 2 раза больше, чем у Сауле:
Подставим 4у вместо х, и решим ур-ние относительно у:
Чтобы избавиться от знаменателя, умножим обе части ур-я на y+52:
Перенесем свободные члены и неизвестные в разные части ур-я
тогда у Асем было в 4 раза больше: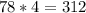 .
.
Теперь проверим решения, подсчитав количество открыток после того, как Асем поделилась открытками с подружкой. Она отдала 52 открытки, а Сауле получила 52 открытки
Как и сказано в условии, у Асем стало в два раза больше открыток, чем у Сауле.
Решение выполнено правильно
Число {\displaystyle \pi }\pi иррационально, то есть его значение не может быть точно выражено в виде дроби {\displaystyle {\frac {m}{n}}}{\frac {m}{n}}, где {\displaystyle m}m — целое число, а {\displaystyle n}n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. Иррациональность числа {\displaystyle \pi }\pi была впервые доказана Иоганном Ламбертом в 1761 году[2] путём разложения тангенса в непрерывную дробь. В 1794 году Лежандр привёл более строгое доказательство иррациональности чисел {\displaystyle \pi }\pi и {\displaystyle \pi ^{2}}\pi ^{2}. Несколько доказательств подробно приведено в статье Доказательства иррациональности π.
{\displaystyle \pi }\pi — трансцендентное число, то есть оно не может быть корнем какого-либо многочлена с целыми коэффициентами. Трансцендентность числа {\displaystyle \pi }\pi была доказана в 1882 году профессором Кёнигсбергского, а позже Мюнхенского университета Линдеманом. Доказательство упростил Феликс Клейн в 1894 году[3]. Поскольку в евклидовой геометрии площадь круга и длина окружности являются функциями числа {\displaystyle \pi }\pi , то доказательство трансцендентности {\displaystyle \pi }\pi положило конец попыткам построить квадратуру круга, длившимся более 2,5 тысяч лет.
В 1934 году Гельфонд доказал[4] трансцендентность числа {\displaystyle e^{\pi }}e^{\pi }. В 1996 году Юрий Нестеренко доказал, что для любого натурального {\displaystyle n}n числа {\displaystyle \pi }\pi и {\displaystyle e^{\pi {\sqrt {ne^{\pi {\sqrt {n}}} алгебраически независимы, откуда, в частности, следует[5][6] трансцендентность чисел {\displaystyle \pi +e^{\pi },\pi e^{\pi }}\pi +e^{\pi },\pi e^{\pi } и {\displaystyle e^{\pi {\sqrt {ne^{\pi {\sqrt {n}}}.
{\displaystyle \pi }\pi является элементом кольца периодов (а значит, вычислимым и арифметическим числом). Но неизвестно, принадлежит ли {\displaystyle 1/\pi }1/\pi к кольцу периодов.