Первым делом найдем все возможные делители чисел (6 ; 15). Нужно поочередно разделить число 6 на делители от 1 до 6, число 15 на делители от 1 до 15. Если число делится без остатка, то делитель запишем в список делителей.
Для числа 6 выпишем все случаи, когда оно делится без остатка:
6 : 1 = 6; 6 : 2 = 3; 6 : 3 = 2; 6 : 6 = 1;
Для числа 15 выпишем все случаи, когда оно делится без остатка:
15 : 1 = 15; 15 : 3 = 5; 15 : 5 = 3; 15 : 15 = 1;
Потом нужно выписать все общие делители чисел (6 ; 15) и выделть самый большой, это и будет наибольший общий делитель НОД чисел (6 ; 15)
Общие делители чисел (6 ; 15): 1, 3
Следовательно ответ такой: НОД (6 ; 15) = 3
НОК (Наименьшее общее кратное)
Перввым делом разложим числа на простые множители. Нужно проверить, является ли каждое из чисел простым (если число простое, то его не получится разложить на простые множители, и оно само является своим разложением)
15 - составное число; 6 - составное число
Разложим число 15 на простые множители . Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
15 : 3 = 5 - делится на простое число 3.
Завершаем деление, так как 5 простое число
Разложим число 6 на простые множители. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
6 : 2 = 3 - делится на простое число 2.
Завершаем деление, так как 3 простое число
Прежде всего запишем множители самого большого числа, а затем меньшего числа. Найдем недостающие множители в разложении меньшего числа множители, которые не вошли в разложение большего числа.
15 = 3 ∙ 5
6 = 2 ∙ 3
Теперь, чтобы найти НОК нужно перемножить множители большего числа с недостающими множителями.
На русском:
Запиши дроби цифрами: пять девятых; шесть десятых; семнадцать двадцать восьмых; сорок три сотых.
Назови числитель и знаменатель каждой дроби.
Что обозначает знаменатель дроби? Числитель дроби?
Задание:
Числитель: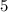
Знаменатель: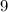
Числитель: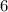
Знаменатель: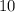
Числитель: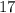
Знаменатель:
Числитель: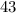
Знаменатель: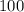
Знаменатель стоит под дробной чертой. Оно указывает, на сколько равных частей поделили число.
Числитель стоит над дробной чертой. Он указывает, сколько долей содержится в дроби.
На украиснком:
Запиши дроби цифрами: п'ять дев'ятих; шість десятих; сімнадцять двадцять восьмих; сорок три сотих.
Назви чисельник і знаменник кожного дробу.
Що позначає знаменник дробу? Чисельник дробу?
Завдання:
Чисельник: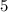
Знаменник: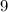
Чисельник: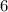
Знаменник: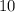
Чисельник: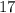
Знаменник:
Чисельник: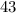
Знаменник: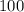
Знаменник стоїть під дробової рисою. Воно вказує, на скільки рівних частин поділили число.
Чисельник стоїть над дробової рисою. Він вказує, скільки часток міститься в дробу.
НОД (Наибольший общий делитель)
Первым делом найдем все возможные делители чисел (6 ; 15). Нужно поочередно разделить число 6 на делители от 1 до 6, число 15 на делители от 1 до 15. Если число делится без остатка, то делитель запишем в список делителей.
Для числа 6 выпишем все случаи, когда оно делится без остатка:
6 : 1 = 6; 6 : 2 = 3; 6 : 3 = 2; 6 : 6 = 1;
Для числа 15 выпишем все случаи, когда оно делится без остатка:
15 : 1 = 15; 15 : 3 = 5; 15 : 5 = 3; 15 : 15 = 1;
Потом нужно выписать все общие делители чисел (6 ; 15) и выделть самый большой, это и будет наибольший общий делитель НОД чисел (6 ; 15)
Общие делители чисел (6 ; 15): 1, 3
Следовательно ответ такой: НОД (6 ; 15) = 3
НОК (Наименьшее общее кратное)
Перввым делом разложим числа на простые множители. Нужно проверить, является ли каждое из чисел простым (если число простое, то его не получится разложить на простые множители, и оно само является своим разложением)
15 - составное число; 6 - составное число
Разложим число 15 на простые множители . Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
15 : 3 = 5 - делится на простое число 3.
Завершаем деление, так как 5 простое число
Разложим число 6 на простые множители. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
6 : 2 = 3 - делится на простое число 2.
Завершаем деление, так как 3 простое число
Прежде всего запишем множители самого большого числа, а затем меньшего числа. Найдем недостающие множители в разложении меньшего числа множители, которые не вошли в разложение большего числа.
15 = 3 ∙ 5
6 = 2 ∙ 3
Теперь, чтобы найти НОК нужно перемножить множители большего числа с недостающими множителями.
Следовательно, ответ такой: НОК (15 ; 6) = 3 ∙ 5 ∙ 2 = 30
Думаю, ты понял(а) как решать, так что дальше буду писать просто ответы..
НОД (15 ; 20) = 5
НОК (20 ; 15) = 60
НОД (1 ; 20) = 1
НОК (20 ; 1) = 20
НОД (168 ; 2) = 2
НОК (168 ; 2) = 168
НОД (3 ; 27) = 3
НОК (27 ; 3) = 27
Все... фух рука устала писать