Допустим, что число - бесконечная периодическая дробь. Тогда, начиная с -ой цифры, некоторая последовательность из цифр будет повторяться бесконечно. Очевидно, что, после -ой цифры найдутся ненулевые цифры. А значит искомый период длины содержит хотя бы одну ненулевую цифру.
Также очевидно, что в десятичной записи присутствует число . В нем одна 1, а за ней следуют нулей.
Пусть в период входят одна 1 и нулей этого числа. Но следующие цифр - нули (т.к. в предыдущее повторение периода вошло меньше, чем нулей, незадействованными остались подряд идущих нулей) - противоречие с тем, что в периоде есть ненулевая цифра.
А значит у дроби нет периода.
Т.к. она бесконечная (число натуральных чисел бесконечно), то иррациональная.
Допустим, что число - бесконечная периодическая дробь. Тогда, начиная с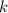 -ой цифры, некоторая последовательность из
-ой цифры, некоторая последовательность из 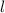 цифр будет повторяться бесконечно. Очевидно, что, после
цифр будет повторяться бесконечно. Очевидно, что, после 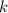 -ой цифры найдутся ненулевые цифры. А значит искомый период длины
-ой цифры найдутся ненулевые цифры. А значит искомый период длины 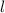 содержит хотя бы одну ненулевую цифру.
содержит хотя бы одну ненулевую цифру.
Также очевидно, что в десятичной записи присутствует число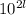 . В нем одна 1, а за ней следуют
. В нем одна 1, а за ней следуют 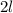 нулей.
нулей.
Пусть в период входят одна 1 и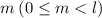 нулей этого числа. Но следующие
нулей этого числа. Но следующие 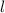 цифр - нули (т.к. в предыдущее повторение периода вошло меньше, чем
цифр - нули (т.к. в предыдущее повторение периода вошло меньше, чем 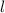 нулей, незадействованными остались
нулей, незадействованными остались 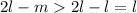 подряд идущих нулей) - противоречие с тем, что в периоде есть ненулевая цифра.
подряд идущих нулей) - противоречие с тем, что в периоде есть ненулевая цифра.
А значит у дроби нет периода.
Т.к. она бесконечная (число натуральных чисел бесконечно), то иррациональная.
ответ: число иррационально