ДАНО:
Исследование:
1. Область определения D(y). В знаменателе: 2*х+1 ≠0, х≠ - 0,5
Х∈(-∞;-0,5)∪(-0,5+∞) -
2, Непрерывность функции: разрыв при Х=-0,5.
Вертикальная асимптота: х = -0,5.
3. Проверка на чётность.
Y(-x) = (x²+3)/(-2*x+1) ≠ - Y(x) ≠ Y(x)
Функция ни чётная ни нечётная.
Вывод: нет ни осевой симметрии, как у функции y = x², ни центральной, как у функции y= x³
4. Пересечение с осью OХ. Y(x) = 0 - нет.
5. Интервалы знакопостоянства.
Отрицательная - Y(x)<0 X=(-oo;-0,5]
Положительная -Y(x)>0 X=[-0,5;+oo)
6. Пересечение с осью OY. Y(0) = 3.
7. Поиск экстремумов по первой производной.
Корни Y'(x)= 0. Х4= 2x/2x = 1 Х5= ? (≈-2.25)
7. Локальные экстремумы.
Минимум Ymin(X4= 1) =4/3. Максимум Ymin(X5=8,36) = ?
8. Интервалы возрастания и убывания.
Возрастает Х=(-оо; x5]U[1;+oo) , убывает - Х=[x5;-0.5)∪(0.5;1]
9. Вторая производная
Корней производной - нет. Точка перегиба в точке разрыва при Х=-0,5
10. Выпуклая “горка» Х∈(-∞; -0,5)
Вогнутая – «ложка» Х∈(-0,5; +∞).
11. График в приложении.
Клоуны с хлопушками.
Веселится весь народ!
Что за праздник? (Новый год)
В нем двенадцать месяцев
Запросто уместятся.
Всех их вместе соберет
Одно слово, это... (год)
Украшена игрушками,
Шарами и хлопушками —
Не пальма, не сосеночка,
А праздничная... (елочка)
Он с подарками приходит,
Хороводы с нами водит.
Белой бородой оброс
Добрый Дедушка... (Мороз)
К детям в гости Дед Мороз
Внучку на санях привез.
Снежная фигурка —
К нам придет... (Снегурка)
И в коробки, и в пакеты
Упакованы конфеты.
Фантики так ярки!
Будут всем... (подарки)
Целый год лежал на полке,
А теперь висит на елке.
Это не фонарик,
А стеклянный... (шарик)
Быстро огоньки мигают,
Сверху вниз перебегают.
Эта дружная команда
Называется... (гирлянда)
На красавице лесной
Золотится дождь волной —
С серебристого шнура
Вниз свисает... (мишура)
Вьюга по двору гуляет,
В доме елочка сверкает.
Дети водят хоровод.
Что за праздник? (Новый год)
Вся в огнях большая елка,
Вверх летят петарды звонко.
Снег на улице идет.
Наступает... (Новый год)
Все на елочке игрушки:
Бусы, шарики, хлопушки.
Ребятня подарков ждет.
Что за праздник? (Новый год)
Меня не растили.
Из снега слепили.
Вместо носа ловко вставили морковку.
Глаза — угольки.
Руки — сучки.
Холодная, большая,
Кто я такая? (Снежная баба)
Он приходит в зимний вечер
Зажигать на елке свечи.
Бородой седой оброс,
Кто же это? (Дед Мороз)
Мы купили вешалку
С звездою на макушке.
Повесили на вешалку
Не шапки, а игрушки! (Ёлка)
ДАНО: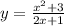
Исследование:
1. Область определения D(y). В знаменателе: 2*х+1 ≠0, х≠ - 0,5
Х∈(-∞;-0,5)∪(-0,5+∞) -
2, Непрерывность функции: разрыв при Х=-0,5.
Вертикальная асимптота: х = -0,5.
3. Проверка на чётность.
Y(-x) = (x²+3)/(-2*x+1) ≠ - Y(x) ≠ Y(x)
Функция ни чётная ни нечётная.
Вывод: нет ни осевой симметрии, как у функции y = x², ни центральной, как у функции y= x³
4. Пересечение с осью OХ. Y(x) = 0 - нет.
5. Интервалы знакопостоянства.
Отрицательная - Y(x)<0 X=(-oo;-0,5]
Положительная -Y(x)>0 X=[-0,5;+oo)
6. Пересечение с осью OY. Y(0) = 3.
7. Поиск экстремумов по первой производной.
Корни Y'(x)= 0. Х4= 2x/2x = 1 Х5= ? (≈-2.25)
7. Локальные экстремумы.
Минимум Ymin(X4= 1) =4/3. Максимум Ymin(X5=8,36) = ?
8. Интервалы возрастания и убывания.
Возрастает Х=(-оо; x5]U[1;+oo) , убывает - Х=[x5;-0.5)∪(0.5;1]
9. Вторая производная
Корней производной - нет. Точка перегиба в точке разрыва при Х=-0,5
10. Выпуклая “горка» Х∈(-∞; -0,5)
Вогнутая – «ложка» Х∈(-0,5; +∞).
11. График в приложении.