0в спортивную группу входят 9 лыжников, 8 конькобежцев,7 бегунов,11 прыгунов найти вероятность,что среди на удачу отобраны 6 спортсменов все лыжники 1 из коробки где 5 зеленых и 4 красных наудачу одновременно извлекают 3 шара найти вероятность что извлеченные шары будут одного цвета 2 из 2 коробок: в первой- 2 желтых и 4 черных во –второй 3 желтых и 5 черных. из первой коробки во вторую перекладывают,не глядя, один шар. после перемешивают из второй коробки вынимают один шар. найти вероятность,что этот шар черный
Всего в спортивной группе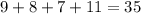 человек.
человек.
Из них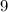 - лыжники.
- лыжники.
P (первый выбранный - лыжник) =И все эти вероятности нужно перемножить, чтобы получить ту вероятность, которую нас просят в задаче:
P (все выбранные люди - лыжники) =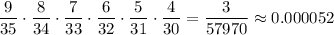 .
.
Задача 1.P (все извлеченные шары одного цвета) = P (все извлеченные шары зеленые) + P (все извлеченные шары - красные).
P (все извлеченные шары - зеленые) =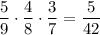 .
.
P (все извлеченные шары - красные) =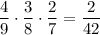 .
.
P (искомая) =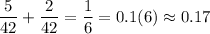 .
.
Задача 2.Искомую вероятность опять можно получить сложением двух других вероятностей:
P₁ = P (из первой коробки достали именно черный шар) · P (из второй коробки, в которой уже на 1 черный шар больше, тоже достали черный шар) =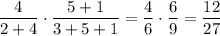 .
.
P₂ = P (из первой коробки был извлечен желтый шар) · P (из второй, в которой теперь на 1 желтый шар больше, достали все же черный шар) =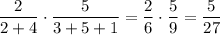 .
.
P (искомая) =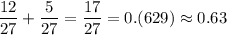 .
.