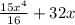1) (160597-261+14474+1269010+47086+44015)6: 11117146 2) (43489-71-70-61-169-80+40962-316)6+34736-11737 3) (10192+1565+37314+46830-120+10351-257)6+29257+46457-2428 4) (13359: 61+47740)6+23926-271-1205-778-(1112+1068)*7

Показать ответ

Ответ:

zorlnaviitukp00zmd

04.07.2022 11:48

К задаче есть два решения:

1. Решение по действиям (их будет два).

1-е действие - вычисляем сколько всего комнат:

1 )17*4 = 68 (кв) - всего комнат.

2-е действие - считаем сколько осталось комнат:

2) 68-19 = 49 (комнат) - осталось отремонтировать.

И так, мы закончили с первым решения - переходим ко второму)

2.Задачу можно решить одним действием. (Но при таком надо соблюдать порядок вычисления)

17*4-19 - вот такое выражение будет, если решать в одно действие.

Если вы путаетесь, решайте постепенно:

17*4-19=68-19=49 (комнат) - осталось отремонтировать.

Если нет считайте сразу:

17*4-19=49 (комнат) - осталось отремонтировать.

Мы рассмотрели два решения этой задачи, запишем ответ:

ответ: 49 комнат осталось отремонтировать

0,0(0 оценок)

Ответ:

qazdhnvd

29.01.2023 15:28

Пошаговое объяснение:

1) с первым интегралом все достаточно просто

здесь мы перейдем к повторным интегралам и получим вот что

$\int\limits^3_1 {} \, dy \int\limits^1_0 {\frac{y^2}{1+x^2} } \, dx$

сначала вычисляем внутренний интеграл

$\int\limits^1_0 {\frac{y^2}{x^2+1} } \, dx = y^2arctgxI_0^1=\frac{\pi y^2}{4}$

теперь вычисляем внешний интеграл

$\int\limits^3_1 {\frac{\pi y^2}{4} } \, dy =\frac{\pi y^3}{12} I_1^3=\frac{13\pi }{6}$

это и есть ответ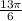 $\frac{13\pi }{6}$

2) со вторым придется построить графики, чтобы определить границы интегрирования по х

тут мы видим, что х изменяется 0≤х≤4

в общем-то нижний предел интегрирования можно было бы найти и путем выяснения, в какой точке пересекаются графики (через уравнение х/2 = х корень данного уравнения х=0), но лучше все же строить график

теперь, собственно приступаем к переходу и интеграции

$\int\limits^x_{\frac{x}{2} } {} \, dy\int\limits^4_0 {(x^3+y^3)} \, dx$