В скобке правой части сумма арифметической прогрессии с разностью, равной 1 и первым членом 1, ее сумма равна (1+n)*n/2, поскольку скобка справа в квадрате, то (1 + 2 + ... + n)²= ((1+n)*n/2)²=
(1+n)²*n²/4, значит, нужно доказать, что 1³ + 2³ + ... + n³ = (1+n)²*n²/4,
Доказать утверждение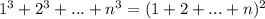 методом математической индукции.
методом математической индукции.
В скобке правой части сумма арифметической прогрессии с разностью, равной 1 и первым членом 1, ее сумма равна (1+n)*n/2, поскольку скобка справа в квадрате, то (1 + 2 + ... + n)²= ((1+n)*n/2)²=
(1+n)²*n²/4, значит, нужно доказать, что 1³ + 2³ + ... + n³ = (1+n)²*n²/4,
1. Берем n=1 /база/, проверяем справедливость равенства.1³=2²*1²/4=1
2. Предполагаем, что для n=к равенство выполняется.
т.е. 1³ + 2³ + ... + к³ = (1+к)²*к²/4
3. Докажем, что для n= к+1 равенство выполняется. т.е., что
1³ + 2³ + ... + (к+1)³ = (1+к)²*(2+к)²/4
(1³ + 2³ + ... к³)+ (к+1)³ =(1+к)²*к²/4+ (к+1)³=(к+1)²*(к²+4к+4)/4=(1+к)²*(2+к)²/4
Доказано.