1)3^х+2 + 3^х = 30 2)2/lgx-3 + 4/lgx+1 = 1

1)3^(х+2) + 3^х = 30

3^х ·3^2 + 3^х = 30

3^х ·9 + 3^х = 30

3^х ·(9 + 1) = 30

10·3^х  = 30

3^х  = 3

x = 1

2) 2/(lgx-3) + 4/(lgx+1) = 1

ОДЗ: lgx ≠ 3, lgx ≠ 1, х > 0

2·(lgx+1)/((lgx-3)·(lgx+1)) + 4·(lgx-3)/((lgx+1)(lgx-3)) = ((lgx+1)(lgx-3))/((lgx+1)(lgx-3))

2·(lgx+1) + 4·(lgx-3) = (lgx+1)(lgx-3)

2lgx + 2 + 4lgx -12 = lg²x + lgx - 3lgx - 3

6lgx -10 = lg²x - 2lgx - 3

  lg²x - 8lgx + 7 = 0

Замена: у = lgx

  у² - 8у + 7 = 0

D = 64 - 28 = 36

√D = 6

y₁ = (8 - 6):2 = 1

y₂ = (8 + 6):2 = 7

Возвращаемся к замене

1) 1 = lgx

х₁ = 10

2) 7 = lgx

х₂ = 10⁷ = 10 000 000

1) 

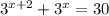
x=1

ответ: х=1 

2)  

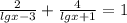
ОДЗ: x#1000,  x#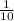 

2lgx+2+4lgx-12=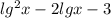 

lgx=7 ,                                                     lgx=1

x=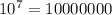 ,                x=10

Оба корня удовлетворяют ОДЗ, значит это и есть ответ